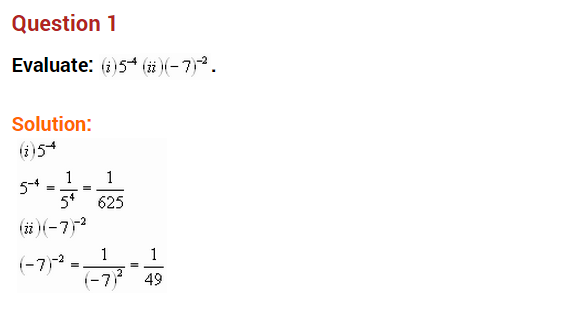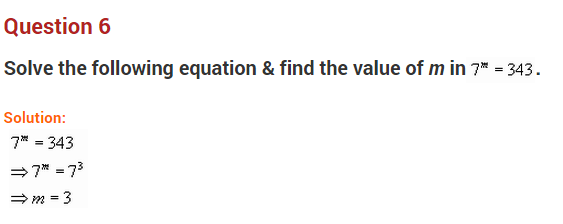Extra Questions for Class 8 Maths Chapter 12 Exponents and Powers

Exponents and Powers Class 8 Extra Questions Very Short Answer Type

Question 1.
Find the multiplicative inverse of:
(i) 3^-3
(ii) 10^-10
Solution:

Question 2.
Expand the following using exponents.
(i) 0.0523
(ii) 32.005
Solution:

Question 3.
Simplify and write in exponential form.

Solution:

Question 4.
Simplify the following and write in exponential form.

Solution:

Question 5.
Express 8^-4 as a power with the base 2.
Solution:
We have 8 = 2 × 2 × 2 = 2³
8^-4 = (2³)^-4 = 2^3×(-4) = 2^-12

Question 6.
Simplify the following and write in exponential form.
(i) (3⁶ ÷ 3⁸)⁴ × 3^-4
(ii) \(\frac { 1 }{ 27 }\) × 3^-3
Solution:

Question 7.
Find the value of k if (-2)^k+1 × (-2)³ = (-2)⁷
Solution:
(-2)^k+1 × (-2)³ = (-2)⁷
⇒ (-2)^k+1+3 = (-2)⁷
⇒ (-2)^k+4 = (-2)⁷
⇒ k + 4 = 7
⇒ k = 3
Hence, k = 3.

Question 8.
Simplify the following:

Solution:

Question 9.
Find the value of \(\left[ \left( -\frac { 3 }{ 4 } \right) ^{ -2 } \right] ^{ 2 }\)
Solution:

Question 10.
Write the following in standard form
(i) 0 0035
(ii) 365.05
Solution:

Exponents and Powers Class 8 Extra Questions Short Answer Type

Question 11.
Find the value of P if

Solution:

Question 12.

Solution:

Question 13.
Find the value of x if

Solution:

⇒ 3 + x = 18 [Equating the powers of same base]
x = 18 – 3 = 15

Question 14.
Solve the following: (81)^-4 ÷ (729)^2-x = 9^4x
Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.
Find x so that (-5)^x+1 × (-5)⁵ = (-5)⁷ (NCERT Exemplar)
Solution:
(-5)^x+1 × (-5)⁵ = (-5)⁷
(-5)^x+1+5 = (-5)⁷ {a^m × aⁿ = a^m+n}
(-5)^x+6 = (-5)⁷
On both sides, powers have the same base, so their exponents must be equal.
Therefore, x + 6 = 7
x = 7 – 6 = 1
x = 1.