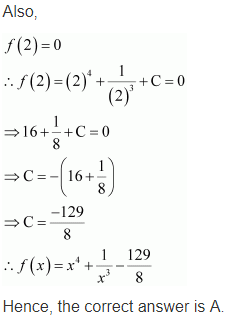Class 12 Maths Chapter 7 NCERT Solutions Integrals

NCERT Solutions for Class 12 Maths Chapter 7 – Integrals contains step-by-step and detailed solutions for every question.

1. Introduction
2. Integration as an Inverse Process of Differentiation
3. Geometrical interpretation of indefinite integral
4. Some properties of indefinite integral
5. Comparison between differentiation and integration
6. Methods of Integration
7. Integration by substitution
8. Integration using trigonometric identities
9. Integrals of Some Particular Functions
10. Integration by Partial Fractions
11. Integration by Parts
12. Integral of the type
13. Integrals of some more types
14. Definite Integral
15. Definite integral as the limit of a sum
16. Fundamental Theorem of Calculus
17. Area function
18. First fundamental theorem of integral calculus
19. Second fundamental theorem of integral calculus
20. Evaluation of Definite Integrals by Substitution
21. Some Properties of Definite Integrals

Integrals Ex 7.1 Class 12

Ex 7.1 Class 12 Maths Question 1.
sin 2x
Solution:

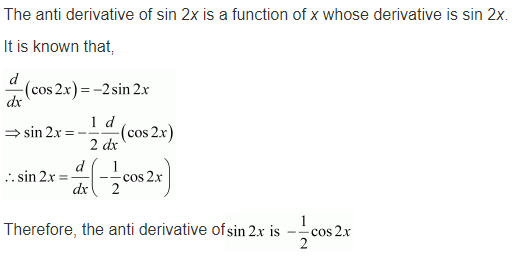
Ex 7.1 Class 12 Maths Question 2.
cos 3x
Solution:

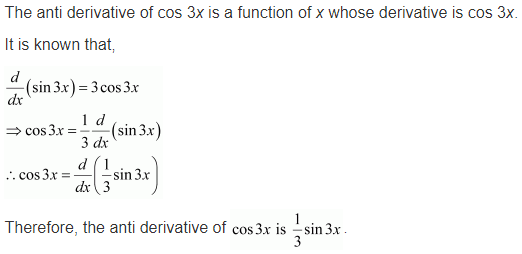
Ex 7.1 Class 12 Maths Question 3.
\({ e }^{ 2x }\)
Solution:

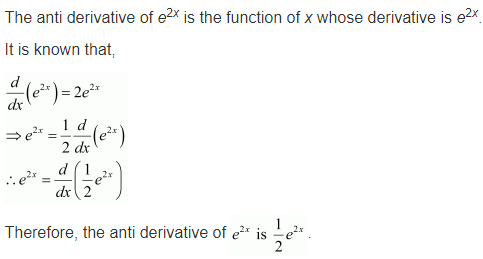
Ex 7.1 Class 12 Maths Question 4.
(ax + c)²
Solution:

Ex 7.1 Class 12 Maths Question 5.
\({ sin\quad 2x-4e }^{ 3x }\)
Ex 7.1 Class 12 Maths Solution:

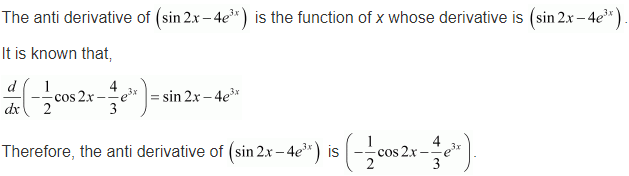
Find the following integrals in Exercises 6 to 20 :

Ex 7.1 Class 12 Maths Question 6.
\(\int { \left( { 4e }^{ 3x }+1 \right) dx } \)
Solution:

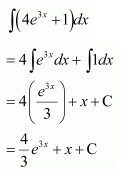
Ex 7.1 Class 12 Maths Question 7.
\(\int { { x }^{ 2 }\left( 1-\frac { 1 }{ { x }^{ 2 } } \right) dx } \)
Solution:

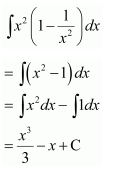
Ex 7.1 Class 12 Maths Question 8.
\(\int { { (ax }^{ 2 }+bx+c)dx } \)
Solution:

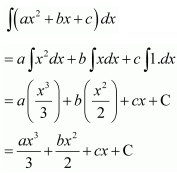
Ex 7.1 Class 12 Maths Question 9.
\(\int { \left( { 2x }^{ 2 }+{ e }^{ x } \right) dx } \)
Solution:

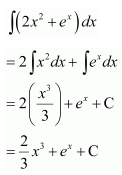
Ex 7.1 Class 12 Maths Question 10.
\(\int { { \left[ \sqrt { x } -\frac { 1 }{ \sqrt { x } } \right] }^{ 2 }dx } \)
Solution:

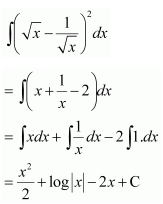
Ex 7.1 Class 12 Maths Question 11.
\(\int { \frac { { x }^{ 3 }+{ 5x }^{ 2 }-4 }{ { x }^{ 2 } } dx } \)
Solution:

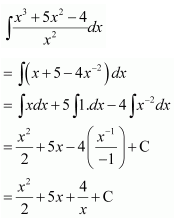
Ex 7.1 Class 12 Maths Question 12.
\(\int { \frac { { x }^{ 3 }+3x+4 }{ \sqrt { x } } dx } \)
Solution:

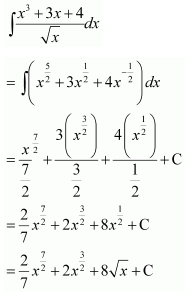
Ex 7.1 Class 12 Maths Question 13.
\(\int { \frac { { x }^{ 3 }-{ x }^{ 2 }+x-1 }{ x-1 } dx } \)
Solution:

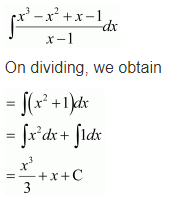
Ex 7.1 Class 12 Maths Question 14.
\(\int { \left( 1-x \right) \sqrt { x } dx } \)
Solution:

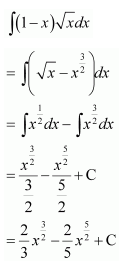
Ex 7.1 Class 12 Maths Question 15.
\(\int { \sqrt { x } \left( { 3x }^{ 2 }+2x+3 \right) dx } \)
Solution:

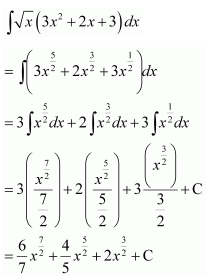
Ex 7.1 Class 12 Maths Question 16.
\(\int { (2x-3cosx+{ e }^{ x })dx } \)
Solution:

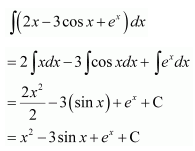
Ex 7.1 Class 12 Maths Question 17.
\(\int { \left( { 2x }^{ 2 }-3sinx+5\sqrt { x } \right) dx } \)
Solution:

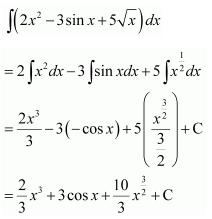
Ex 7.1 Class 12 Maths Question 18.
\(\int { secx(secx+tanx)dx } \)
Solution:

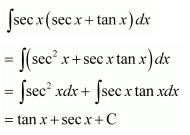
Ex 7.1 Class 12 Maths Question 19.
\(\int { \frac { { sec }^{ 2 }x }{ { cosec }^{ 2 }x } dx } \)
Solution:

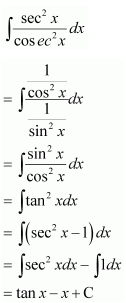
Ex 7.1 Class 12 Maths Question 20.
\(\int { \frac { 2-3sinx }{ { cos }^{ 2 }x } dx } \)
Solution:

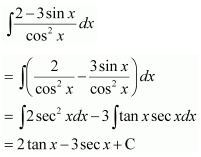
Choose the correct answer in Exercises 21 and 22.
Ex 7.1 Class 12 Maths Question 21.
The antiderivative \(\left( \sqrt { x } +\frac { 1 }{ \sqrt { x } } \right) \) equals
(a) \(\frac { 1 }{ 3 } { x }^{ \frac { 1 }{ 3 } }+{ 2x }^{ \frac { 1 }{ 2 } }+c\)
(b) \(\frac { 2 }{ 3 } { x }^{ \frac { 2 }{ 3 } }+{ \frac { 1 }{ 2 } x }^{ 2 }+c\)
(c) \(\frac { 2 }{ 3 } { x }^{ \frac { 3 }{ 2 } }+{ 2x }^{ \frac { 1 }{ 2 } }+c\)
(d) \(\frac { 3 }{ 2 } { x }^{ \frac { 3 }{ 2 } }+\frac { 1 }{ 2 } { x }^{ \frac { 1 }{ 2 } }+c\)
Solution:

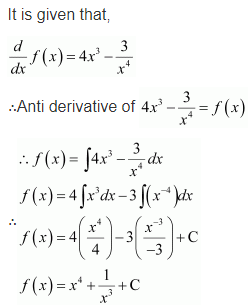
Ex 7.1 Class 12 Maths Question 22.
If \(\frac { d }{ dx } f(x)={ 4x }^{ 3 }-\frac { 3 }{ { x }^{ 4 } } \) such that f(2)=0 then f(x) is
(a) \({ x }^{ 4 }+\frac { 1 }{ { x }^{ 3 } } -\frac { 129 }{ 8 } \)
(b) \({ x }^{ 3 }+\frac { 1 }{ { x }^{ 4 } } +\frac { 129 }{ 8 } \)
(c) \({ x }^{ 4 }+\frac { 1 }{ { x }^{ 3 } } +\frac { 129 }{ 8 } \)
(d) \({ x }^{ 3 }+\frac { 1 }{ { x }^{ 4 } } -\frac { 129 }{ 8 } \)
Solution:

Integrals Ex 7.2 Class 12

Integrate the functions in Exercises 1 to 37:

Ex 7.2 Class 12 Maths Question 1.
\(\frac { 2x }{ 1+{ x }^{ 2 } } \)
Solution:

Ex 7.2 Class 12 Maths Question 2.
\(\frac { { \left( logx \right) }^{ 2 } }{ x } \)
Solution:

Ex 7.2 Class 12 Maths Question 3.
\(\frac { 1 }{ x+xlogx } \)
Solution:

Ex 7.2 Class 12 Maths Question 4.
sinx sin(cosx)
Solution:

Ex 7.2 Class 12 Maths Question 5.
sin(ax+b) cos(ax+b)
Solution:

Ex 7.2 Class 12 Maths Question 6.
\(\sqrt { ax+b } \)
Solution:

Ex 7.2 Class 12 Maths Question 7.
\(x\sqrt { x+2 } \)
Solution:

Ex 7.2 Class 12 Maths Question 8.
\(x\sqrt { 1+{ 2x }^{ 2 } } \)
Solution:

Ex 7.2 Class 12 Maths Question 9.
\((4x+2)\sqrt { { x }^{ 2 }+x+1 } \)
Solution:

Ex 7.2 Class 12 Maths Question 10.
\(\frac { 1 }{ x-\sqrt { x } } \)
Solution:

Ex 7.2 Class 12 Maths Question 11.
\(\frac { x }{ \sqrt { x+4 } } ,x>0\)
Solution:

Ex 7.2 Class 12 Maths Question 12.
\({ { (x }^{ 3 }-1) }^{ \frac { 1 }{ 3 } }.{ x }^{ 5 }\)
Solution:

Ex 7.2 Class 12 Maths Question 13.
\(\frac { { x }^{ 2 } }{ { { (2+3x }^{ 3 }) }^{ 3 } } \)
Solution:

Ex 7.2 Class 12 Maths Question 14.
\(\frac { 1 }{ x(logx)^{ m } } ,x>0\)
Solution:

Ex 7.2 Class 12 Maths Question 15.
\(\frac { x }{ 9-4{ x }^{ 2 } } \)
Solution:

Ex 7.2 Class 12 Maths Question 16.
\({ e }^{ 2x+3 }\)
Solution:

Ex 7.2 Class 12 Maths Question 17.
\(\frac { x }{ { e }^{ { x }^{ 2 } } } \)
Solution:

Ex 7.2 Class 12 Maths Question 18.
\(\frac { { e }^{ { tan }^{ -1 }x } }{ 1+{ x }^{ 2 } } \)
Solution:

Ex 7.2 Class 12 Maths Question 19.
\(\frac { { e }^{ 2x }-1 }{ { e }^{ 2x }+1 } \)
Solution:

Ex 7.2 Class 12 Maths Question 20.
\(\frac { { e }^{ 2x }-{ e }^{ 2x } }{ { e }^{ 2x }+{ e }^{ -2x } } \)
Solution:

Ex 7.2 Class 12 Maths Question 21.
tan²(2x-3)
Solution:
∫tan²(2x-3)dx = ∫[sec²(2x-3)-1]dx = I
put 2x-3 = t
so that 2dx = dt
I = \(\frac { 1 }{ 2 }\) ∫sec²t dt-x+c
= \(\frac { 1 }{ 2 }t-x+c\)
= \(\frac { 1 }{ 2 }tan(2x-3)-x+c\)
Ex 7.2 Class 12 Maths Question 22.
sec²(7-4x)
Solution:

Ex 7.2 Class 12 Maths Question 23.
\(\frac { { sin }^{ -1 }x }{ \sqrt { 1-{ x }^{ 2 } } } \)
Solution:

Ex 7.2 Class 12 Maths Question 24.
\(\frac { 2cosx-3sinx }{ 6cosx+4sinx }\)
Solution:

Ex 7.2 Class 12 Maths Question 25.
\(\frac { 1 }{ { cos }^{ 2 }x{ (1-tanx) }^{ 2 } } \)
Solution:

Ex 7.2 Class 12 Maths Question 26.
\(\frac { cos\sqrt { x } }{ \sqrt { x } } \)
Solution:

Ex 7.2 Class 12 Maths Question 27.
\(\sqrt { sin2x } cos2x\)
Solution:

Ex 7.2 Class 12 Maths Question 28.
\(\frac { cosx }{ \sqrt { 1+sinx } } \)
Solution:

Ex 7.2 Class 12 Maths Question 29.
cotx log sinx
Solution:

Ex 7.2 Class 12 Maths Question 30.
\(\frac { sinx }{ 1+cosx }\)
Solution:

Ex 7.2 Class 12 Maths Question 31.
\(\frac { sinx }{ { (1+cosx) }^{ 2 } } \)
Solution:

Ex 7.2 Class 12 Maths Question 32.
\(\frac { 1 }{ 1+cotx }\)
Solution:

Ex 7.2 Class 12 Maths Question 33.
\(\frac { 1 }{ 1-tanx }\)
Solution:

Ex 7.2 Class 12 Maths Question 34.
\(\frac { \sqrt { tanx } }{ sinxcosx } \)
Solution:

Ex 7.2 Class 12 Maths Question 35.
\(\frac { { (1+logx) }^{ 2 } }{ x } \)
Solution:

Ex 7.2 Class 12 Maths Question 36.
\(\frac { (x+1){ (x+logx) }^{ 2 } }{ x } \)
Solution:

Ex 7.2 Class 12 Maths Question 37.
\(\frac { { x }^{ 3 }sin({ tan }^{ -1 }{ x }^{ 4 }) }{ 1+{ x }^{ 8 } } dx \)
Solution:

Choose the correct answer in exercises 38 and 39

Ex 7.2 Class 12 Maths Question 38.
\(\int { \frac { { 10x }^{ 9 }+{ 10 }^{ x }log{ e }^{ 10 } }{ { x }^{ 10 }+{ 10 }^{ x } } dx } \)
(a) 10x – x10 + C
(b) 10x + x10 + C
(c) (10x – x10) + C
(d) log (10x + x10) + C
Solution:

Ex 7.2 Class 12 Maths Question 39.
\(\int { \frac { dx }{ { sin }^{ 2 }x{ \quad cos }^{ 2 }x } = } \)
(a) tanx + cotx + c
(b) tanx – cotx + c
(c) tanx cotx + c
(d) tanx – cot2x + c
Solution:

Move to Top → Class 12 Integrals Chapter 7

Integrals Ex 7.3 Class 12

Find the integrals of the functions in Exercises 1 to 22.
Ex 7.3 Class 12 Maths Question 1.
sin²(2x+5)
Solution:

Ex 7.3 Class 12 Maths Question 2.
sin3x cos4x
Solution:

Ex 7.3 Class 12 Maths Question 3.
∫cos2x cos4x cos6x dx
Solution:

Ex 7.3 Class 12 Maths Question 4.
∫sin³(2x+1)dx
Solution:

Ex 7.3 Class 12 Maths Question 5.
sin³x cos³x
Solution:

Ex 7.3 Class 12 Maths Question 6.
sinx sin2x sin3x
Solution:

Ex 7.3 Class 12 Maths Question 7.
sin 4x sin 8x
Solution:

Ex 7.3 Class 12 Maths Question 8.
\(\frac { 1-cosx }{ 1+cosx }\)
Solution:

Ex 7.3 Class 12 Maths Question 9.
\(\frac { cosx }{ 1+cosx }\)
Solution:

Ex 7.3 Class 12 Maths Question 10.
∫sinx⁴ dx
Solution:

Ex 7.3 Class 12 Maths Question 11.
cos⁴ 2x
Solution:

Ex 7.3 Class 12 Maths Question 12.
\(\frac { { sin }^{ 2 }x }{ 1+cosx } \)
Solution:

Ex 7.3 Class 12 Maths Question 13.
\(\frac { cos2x-cos2\alpha }{ cosx-cos\alpha } \)
Solution:

Ex 7.3 Class 12 Maths Question 14.
\(\frac { cosx-sinx }{ 1+sin2x }\)
Solution:

Ex 7.3 Class 12 Maths Question 15.
\(\int { { tan }^{ 3 }2x\quad sec2x\quad dx=I } \)
Solution:

Ex 7.3 Class 12 Maths Question 16.
tan⁴x
Solution:

Ex 7.3 Class 12 Maths Question 17.
\(\frac { { sin }^{ 3 }x+{ cos }^{ 3 }x }{ { sin }^{ 2 }x{ cos }^{ 2 }x } \)
Solution:

Ex 7.3 Class 12 Maths Question 18.
\(\frac { cos2x+{ 2sin }^{ 2 }x }{ { cos }^{ 2 }x } \)
Solution:

Ex 7.3 Class 12 Maths Question 19.
\(\frac { 1 }{ sinx{ cos }^{ 3 }x } \)
Solution:

Ex 7.3 Class 12 Maths Question 20.
\(\frac { cos2x }{ { (cosx+sinx) }^{ 2 } } \)
Solution:

Ex 7.3 Class 12 Maths Question 21.
sin^-1 (cos x)
Solution:


Ex 7.3 Class 12 Maths Question 22.
\(\int { \frac { 1 }{ cos(x-a)cos(x-b) } dx } \)
Solution:

Ex 7.3 Class 12 Maths Question 23.
\(\int { \frac { { sin }^{ 2 }x-{ cos }^{ 2 }x }{ { sin }^{ 2 }x{ cos }^{ 2 }x } } dx\quad is\quad equal\quad to\)
(a) tanx+cotx+c
(b) tanx+cosecx+c
(c) -tanx+cotx+c
(d) tanx+secx+c
Solution:

Ex 7.3 Class 12 Maths Question 24.
\(\int { \frac { e^{ x }(1+x) }{ cos^{ 2 }({ e }^{ x }.{ x }) } } dx\quad is\quad equal\quad to\)
(a) -cot(e.x^x)+c
(b) tan(xe^x)+c
(c) tan(e^x)+c
(d) cot e^x+c
Solution:

Integrals Class 12 Ex 7.4

Ex 7.4 Class 12 Maths Question 1.
\(\frac { { 3x }^{ 2 } }{ { x }^{ 6 }+1 } \)
Solution:

Ex 7.4 Class 12 Maths Question 2.
\(\frac { 1 }{ \sqrt { 1+{ 4x }^{ 2 } } } \)
Solution:

Ex 7.4 Class 12 Maths Question 3.
\(\frac { 1 }{ \sqrt { { (2-x) }^{ 2 }+1 } } \)
Solution:

Ex 7.4 Class 12 Maths Question 4.
\(\frac { 1 }{ \sqrt { 9-{ 25x }^{ 2 } } } \)
Solution:

Ex 7.4 Class 12 Maths Question 5.
\(\frac { 3x }{ 1+{ 2x }^{ 4 } } \)
Solution:

Ex 7.4 Class 12 Maths Question 6.
\(\frac { { x }^{ 2 } }{ 1-{ x }^{ 6 } } \)
Solution:

Ex 7.4 Class 12 Maths Question 7.
\(\frac { x-1 }{ \sqrt { { x }^{ 2 }-1 } } \)
Solution:

Ex 7.4 Class 12 Maths Question 8.
\(\frac { { x }^{ 2 } }{ \sqrt { { x }^{ 6 }+{ a }^{ 6 } } } \)
Solution:

Ex 7.4 Class 12 Maths Question 9.
\(\frac { { sec }^{ 2 }x }{ \sqrt { { tan }^{ 2 }x+4 } } \)
Solution:

Ex 7.4 Class 12 Maths Question 10.
\(\frac { 1 }{ \sqrt { { x }^{ 2 }+2x+2 } } \)
Solution:

Ex 7.4 Class 12 Maths Question 11.

\(\frac { 1 }{ { 9x }^{ 2 }+6x+5 } \)
Solution:

Ex 7.4 Class 12 Maths Question 12.
\(\frac { 1 }{ \sqrt { 7-6x-{ x }^{ 2 } } } \)
Solution:

Ex 7.4 Class 12 Maths Question 13.
\(\frac { 1 }{ \sqrt { (x-1)(x-2) } } \)
Solution:

Ex 7.4 Class 12 Maths Question 14.
\(\frac { 1 }{ \sqrt { 8+3x-{ x }^{ 2 } } } \)
Solution:

Ex 7.4 Class 12 Maths Question 15.
\(\frac { 1 }{ \sqrt { (x-a)(x-b) } } \)
Solution:

Ex 7.4 Class 12 Maths Question 16.
\(\frac { 4x+1 }{ \sqrt { { 2x }^{ 2 }+x-3 } } \)
Solution:

Ex 7.4 Class 12 Maths Question 17.
\(\frac { x+2 }{ \sqrt { { x }^{ 2 }-1 } } \)
Solution:


Ex 7.4 Class 12 Maths Question 18.
\(\frac { 5x-2 }{ 1+2x+{ 3x }^{ 2 } } \)
Solution:
put 5x-2=A\(\frac { d }{ dx }\)(1+2x+3x²)+B
⇒ 6A=5, A=\(\frac { 5 }{ 6 }-2=2A+B\), B=\(-\frac { 11 }{ 3 }\)

Ex 7.4 Class 12 Maths Question 19.
\(\frac { 6x+7 }{ \sqrt { (x-5)(x-4) } } \)
Solution:



Ex 7.4 Class 12 Maths Question 20.
\(\frac { x+2 }{ \sqrt { 4x-{ x }^{ 2 } } } \)
Solution:



Ex 7.4 Class 12 Maths Question 21.
\(\frac { x+2 }{ \sqrt { { x }^{ 2 }+2x+3 } } \)
Solution:


Ex 7.4 Class 12 Maths Question 22.
\(\frac { x+3 }{ { x }^{ 2 }-2x-5 } \)
Solution:


Ex 7.4 Class 12 Maths Question 23.
\(\frac { 5x+3 }{ \sqrt { { x }^{ 2 }+4x+10 } } \)
Solution:


Ex 7.4 Class 12 Maths Question 24.
\(\int { \frac { dx }{ { x }^{ 2 }+2x+2 } equals } \)
(a) xtan^-1(x+1)+c
(b) (x+1)tan^-1x+c
(c) tan^-1(x+1)+c
(d) tan^-1x+c
Solution:

Ex 7.4 Class 12 Maths Question 25.
\(\int { \frac { dx }{ \sqrt { 9x-{ 4x }^{ 2 } } } equals } \)
(a) \(\frac { 1 }{ 9 } { sin }^{ -1 }\left( \frac { 9x-8 }{ 8 } \right) +c\)
(b) \(\frac { 1 }{ 2 } { sin }^{ -1 }\left( \frac { 8x-9 }{ 9 } \right) +c\)
(c) \(\frac { 1 }{ 3 } { sin }^{ -1 }\left( \frac { 9x-8 }{ 8 } \right) +c\)
(d) \({ sin }^{ -1 }\left( \frac { 9x-8 }{ 9 } \right) +c\)
Solution:

Move to Top → Class 12 Integrals Chapter 7

Integrals Class 12 Ex 7.5

Ex 7.5 Class 12 Maths Question 1.
\(\frac { x }{ (x+1)(x+2) }\)
Solution:

Ex 7.5 Class 12 Maths Question 2.
\(\frac { 1 }{ { x }^{ 2 }-9 } \)
Solution:

Ex 7.5 Class 12 Maths Question 3.
\(\frac { 3x-1 }{ (x-1)(x-2)(x-3) }\)
Solution:

Ex 7.5 Class 12 Maths Question 4.
\(\frac { x }{ (x-1)(x-2)(x-3) }\)
Solution:

Ex 7.5 Class 12 Maths Question 5.
\(\frac { 2x }{ { x }^{ 2 }+3x+2 } \)
Solution:

Ex 7.5 Class 12 Maths Question 6.
\(\frac { 1-{ x }^{ 2 } }{ x(1-2x) } \)
Solution:

Ex 7.5 Class 12 Maths Question 7.
\(\frac { x }{ \left( { x }^{ 2 }+1 \right) \left( x-1 \right) } \)
Solution:


Ex 7.5 Class 12 Maths Question 8.
\(\frac { x }{ { \left( x-1 \right) }^{ 2 }\left( x+2 \right) } \)
Solution:

Ex 7.5 Class 12 Maths Question 9.
\(\frac { 3x+5 }{ { x }^{ 3 }-{ x }^{ 2 }-x+1 } \)
Solution:

Ex 7.5 Class 12 Maths Question 10.
\(\frac { 2x-3 }{ ({ x }^{ 2 }-1)(2x+3) } \)
Solution:

Ex 7.5 Class 12 Maths Question 11.
\(\frac { 5x }{ (x-1)({ x }^{ 2 }-4) } \)
Solution:

Ex 7.5 Class 12 Maths Question 12.
\(\frac { { x }^{ 3 }+x+1 }{ { x }^{ 2 }-1 } \)
Solution:

Ex 7.5 Class 12 Maths Question 13.
\(\frac { 2 }{ (1-x)(1+{ x }^{ 2 }) } \)
Solution:

Ex 7.5 Class 12 Maths Question 14.
\(\frac { 3x-1 }{ { (x+2) }^{ 2 } } \)
Solution:

Ex 7.5 Class 12 Maths Question 15.
\(\frac { 1 }{ { x }^{ 4 }-1 } \)
Solution:

Ex 7.5 Class 12 Maths Question 16.
\(\frac { 1 }{ x({ x }^{ n }+1) } \)
[Hint : multiply numerator and denominator by x^n-1 and put xⁿ = t ]
Solution:


Ex 7.5 Class 12 Maths Question 17.
\(\frac { cosx }{ (1-sinx)(2-sinx) } \)
Solution:

Ex 7.5 Class 12 Maths Question 18.
\(\frac { \left( { x }^{ 2 }+1 \right) \left( { x }^{ 2 }+2 \right) }{ \left( { x }^{ 2 }+3 \right) \left( { x }^{ 2 }+4 \right) } \)
Solution:


Ex 7.5 Class 12 Maths Question 19.
\(\frac { 2x }{ ({ x }^{ 2 }+1)({ x }^{ 2 }+3) } \)
Solution:

Ex 7.5 Class 12 Maths Question 20.
\(\frac { 1 }{ x({ x }^{ 4 }-1) } \)
Solution:

Ex 7.5 Class 12 Maths Question 21.
\(\frac { 1 }{ { e }^{ x }-1 } \)
Solution:

Ex 7.5 Class 12 Maths Question 22.
choose the correct answer in each of the following :
\(\int { \frac { xdx }{ (x-1)(x-2) } equals } \)
(a) \(log\left| \frac { { (x-1) }^{ 2 } }{ x-2 } \right| +c\)
(b) \(log\left| \frac { { (x-2) }^{ 2 } }{ x-1 } \right| +c\)
(c) \(log\left| \left( \frac { x-{ 1 }^{ 2 } }{ x-2 } \right) \right| +c\)
(d) log|(x-1)(x-2)|+c
Solution:

Ex 7.5 Class 12 Maths Question 23.
\(\int { \frac { dx }{ x({ x }^{ 2 }+1) } equals } \)
(a) \(log|x|-\frac { 1 }{ 2 } log({ x }^{ 2 }+1)+c \)
(b) \(log|x|+\frac { 1 }{ 2 } log({ x }^{ 2 }+1)+c \)
(c) \(-log|x|+\frac { 1 }{ 2 } log({ x }^{ 2 }+1)+c\)
(d) \(\frac { 1 }{ 2 } log|x|+log({ x }^{ 2 }+1)+c \)
Solution:

Integrals Class 12 Ex 7.6

Ex 7.6 Class 12 Maths Question 1.
x sinx
Solution:

Ex 7.6 Class 12 Maths Question 2.
x sin3x
Solution:

Ex 7.6 Class 12 Maths Question 3.
\({ x }^{ 2 }{ e }^{ x }\)
Solution:

Ex 7.6 Class 12 Maths Question 4.
x logx
Solution:

Ex 7.6 Class 12 Maths Question 5.
x log2x
Solution:

Ex 7.6 Class 12 Maths Question 6.
\({ x }^{ 2 }logx\)
Solution:

Ex 7.6 Class 12 Maths Question 7.
\(x\quad { sin }^{ -1 }x\)
Solution:

Ex 7.6 Class 12 Maths Question 8.
\(x\quad { tan }^{ -1 }x\)
Solution:

Ex 7.6 Class 12 Maths Question 9.
\(x\quad { cos }^{ -1 }x\)
Solution:


Ex 7.6 Class 12 Maths Question 10.
\({ (sin }^{ -1 }{ x })^{ 2 }\)
Solution:

Ex 7.6 Class 12 Maths Question 11.
\(\frac { x\quad { cos }^{ -1 }x }{ \sqrt { 1-{ x }^{ 2 } } } \)
Solution:

Ex 7.6 Class 12 Maths Question 12.
x sec²x
Solution:

Ex 7.6 Class 12 Maths Question 13.
\({ ta }n^{ -1 }x\)
Solution:

Ex 7.6 Class 12 Maths Question 14.
x(logx)²
Solution:

Ex 7.6 Class 12 Maths Question 15.
(x²+1)logx
Solution:


Ex 7.6 Class 12 Maths Question 16.
\({ e }^{ x }(sinx+cosx)\)
Solution:

Ex 7.6 Class 12 Maths Question 17.
\(\frac { { xe }^{ x } }{ { (1+x) }^{ 2 } } \)
Solution:

Ex 7.6 Class 12 Maths Question 18.
\(\frac { { e }^{ x }(1+sinx) }{ 1+cosx } \)
Solution:


Ex 7.6 Class 12 Maths Question 19.
\({ e }^{ x }\left( \frac { 1 }{ x } -\frac { 1 }{ { x }^{ 2 } } \right) \)
Solution:

Ex 7.6 Class 12 Maths Question 20.
\(\frac { { (x-2)e }^{ x } }{ { (x-1) }^{ 3 } } \)
Solution:

Ex 7.6 Class 12 Maths Question 21.
\({ e }^{ 2x }sinx\)
Solution:

Ex 7.6 Class 12 Maths Question 22.
\({ sin }^{ -1 }\left( \frac { 2x }{ 1+{ x }^{ 2 } } \right) \)
Solution:

Choose the correct answer in exercise 23 and 24

Ex 7.6 Class 12 Maths Question 23.
\(\int { { x }^{ 2 }{ e }^{ { x }^{ 3 } } } dx\quad equals\)
(a) \(\frac { 1 }{ 3 } { e }^{ { x }^{ 3 } }+c\)
(b) \(\frac { 1 }{ 3 } +{ e }^{ { x }^{ 2 } }+c\)
(c) \(\frac { 1 }{ 2 } { e }^{ { x }^{ 3 } }+c\)
(d) \(\frac { 1 }{ 2 } { e }^{ { x }^{ 2 } }+c\)
Solution:

Ex 7.6 Class 12 Maths Question 24.
\(\int { { e }^{ x }secx(1+tanx) } dx\quad equals\)
(a) \({ e }^{ x }cosx+c\)
(b) \({ e }^{ x }secx+c\)
(c) \({ e }^{ x }sinx+c\)
(d) \({ e }^{ x }tanx+c\)
Solution:

Class 12 Integrals Ex 7.7

Integral the function in exercises 1 to 9

Ex 7.7 Class 12 Maths Question 1.
\(\sqrt { 4-{ x }^{ 2 } } \)
Solution:

Ex 7.7 Class 12 Maths Question 2.
\(\sqrt { 1-{ 4x }^{ 2 } } \)
Solution:

Ex 7.7 Class 12 Maths Question 3.
\(\sqrt { { x }^{ 2 }+4x+6 } \)
Solution:

Ex 7.7 Class 12 Maths Question 4.
\(\sqrt { { x }^{ 2 }+4x+1 } \)
Solution:

Ex 7.7 Class 12 Maths Question 5.
\(\sqrt { 1-4x-{ x }^{ 2 } } \)
Solution:

Ex 7.7 Class 12 Maths Question 6.
\(\sqrt { { x }^{ 2 }+4x-5 } \)
Solution:

Ex 7.7 Class 12 Maths Question 7.
\(\sqrt { 1+3x-{ x }^{ 2 } } \)
Solution:

Ex 7.7 Class 12 Maths Question 8.
\(\sqrt { { x }^{ 2 }+3x } \)
Solution:

Ex 7.7 Class 12 Maths Question 9.
\(\sqrt { 1+\frac { { x }^{ 2 } }{ 9 } } \)
Solution:

Choose the correct answer in the Exercises 10 to 11:

Ex 7.7 Class 12 Maths Question 10.
\(\int { \sqrt { 1+{ x }^{ 2 } } } dx\quad is\quad equal\quad to\)
(a) \(\frac { x }{ 2 } \sqrt { 1+{ x }^{ 2 } } +\frac { 1 }{ 2 } log|x+\sqrt { 1+{ x }^{ 2 } } |+c\)
(b) \(\frac { 2 }{ 3 } { \left( 1+{ x }^{ 2 } \right) }^{ \frac { 3 }{ 2 } }+c\)
(c) \(\frac { 2 }{ 3 } x{ \left( 1+{ x }^{ 2 } \right) }^{ \frac { 3 }{ 2 } }+c\)
(d) \(\frac { { x }^{ 2 } }{ 2 } \sqrt { 1+{ x }^{ 2 } } +\frac { 1 }{ 2 } { x }^{ 2 }log\left| x+\sqrt { 1+{ x }^{ 2 } } \right| +c\)
Solution:

Ex 7.7 Class 12 Maths Question 11.
\(\int { \sqrt { { x }^{ 2 }-8x+7 } } dx\quad is\quad equal\quad to\)

Solution:

Class 12 Integrals Ex 7.8

Ex 7.8 Class 12 Maths Question 1.
\(\int _{ a }^{ b }{ x\quad dx } \)
Solution:

Ex 7.8 Class 12 Maths Question 2.
\(\int _{ 0 }^{ 5 }{ (x+1)dx } \)
Solution:

Ex 7.8 Class 12 Maths Question 3.
\(\int _{ 2 }^{ 3 }{ { x }^{ 2 } } dx\)
Solution:

Ex 7.8 Class 12 Maths Question 4.
\(\int _{ 1 }^{ 4 }{ ({ x }^{ 2 }-x) } dx\)
Solution:

Ex 7.8 Class 12 Maths Question 5.
\(\int _{ -1 }^{ 1 }{ { e }^{ x } } dx\quad \)
Solution:

Ex 7.8 Class 12 Maths Question 6.
\(\int _{ 0 }^{ 4 }{ { (x+e }^{ 2x }) } dx\quad \)
Solution:

Class 12 Integrals Ex 7.9

Ex 7.9 Class 12 Maths Question 1.
\(\int _{ -1 }^{ 1 }{ { (x+1 }) } dx\quad \)
Solution:

Ex 7.9 Class 12 Maths Question 2.
\(\int _{ 2 }^{ 3 }{ \frac { 1 }{ x } dx } \)
Solution:

Ex 7.9 Class 12 Maths Question 3.
\(\int _{ 1 }^{ 2 }{ \left( { 4x }^{ 3 }-{ 5x }^{ 2 }+6x+9 \right) dx } \)
Solution:

Ex 7.9 Class 12 Maths Question 4.
\(\int _{ 0 }^{ \frac { \pi }{ 4 } }{ sin2x\quad dx } \)
Solution:

Ex 7.9 Class 12 Maths Question 5.
\(\int _{ 0 }^{ \frac { \pi }{ 2 } }{ cos2x\quad dx } \)
Solution:

Ex 7.9 Class 12 Maths Question 6.
\(\int _{ 4 }^{ 5 }{ { e }^{ x }dx } \)
Solution:

Ex 7.9 Class 12 Maths Question 7.
\(\int _{ 0 }^{ \frac { \pi }{ 4 } }{ tanx\quad dx } \)
Solution:

Ex 7.9 Class 12 Maths Question 8.
\(\int _{ \frac { \pi }{ 6 } }^{ \frac { \pi }{ 4 } }{ cosec\quad xdx } \)
Solution:

Ex 7.9 Class 12 Maths Question 9.
\(\int _{ 0 }^{ 1 }{ \frac { dx }{ \sqrt { 1-{ x }^{ 2 } } } } \)
Solution:

Ex 7.9 Class 12 Maths Question 10.
\(\int _{ 0 }^{ 1 }{ \frac { dx }{ 1+{ x }^{ 2 } } } \)
Solution:

Ex 7.9 Class 12 Maths Question 11.
\(\int _{ 2 }^{ 3 }{ \frac { dx }{ { x }^{ 2 }-1 } } \)
Solution:

Ex 7.9 Class 12 Maths Question 12.
\(\int _{ 0 }^{ \frac { \pi }{ 2 } }{ { cos }^{ 2 } } xdx\)
Solution:

Ex 7.9 Class 12 Maths Question 13.
\(\int _{ 2 }^{ 3 }{ \frac { x }{ { x }^{ 2 }+1 } } dx\)
Solution:

Ex 7.9 Class 12 Maths Question 14.
\(\int _{ 0 }^{ 1 }{ \frac { 2x+3 }{ { 5x }^{ 2 }+1 } dx } \)
Solution:

Ex 7.9 Class 12 Maths Question 15.
\(\int _{ 0 }^{ 1 }{ { xe }^{ { x }^{ 2 } }dx } \)
Solution:

Ex 7.9 Class 12 Maths Question 16.
\(\int _{ 1 }^{ 2 }{ \frac { { 5x }^{ 2 } }{ { x }^{ 2 }+4x+3 } dx } \)
Solution:

Ex 7.9 Class 12 Maths Question 17.
\(\int _{ 0 }^{ \frac { \pi }{ 4 } }{ \left( { 2sec }^{ 2 }x+{ x }^{ 3 }+2 \right) dx } \)
Solution:

Ex 7.9 Class 12 Maths Question 18.
\(\int _{ 0 }^{ \pi }{ \left( { sin }^{ 2 }\frac { x }{ 2 } -{ cos }^{ 2 }\frac { x }{ 2 } \right) } dx\)
Solution:

Ex 7.9 Class 12 Maths Question 19.
\(\int _{ 0 }^{ 2 }{ \frac { 6x+3 }{ { x }^{ 2 }+4 } } dx\)
Solution:

Ex 7.9 Class 12 Maths Question 20.
\(\int _{ 0 }^{ 1 }{ \left( { xe }^{ x }+sin\frac { \pi x }{ 4 } \right) dx } \)
Solution:

Ex 7.9 Class 12 Maths Question 21.
\(\int _{ 1 }^{ \sqrt { 3 } }{ \frac { dx }{ { 1+x }^{ 2 } } \quad equals } \)
(a) \(\frac { \pi }{ 3 } \)
(b) \(\frac { 2\pi }{ 3 } \)
(c) \(\frac { \pi }{ 6 } \)
(d) \(\frac { \pi }{ 12 } \)
Solution:

Ex 7.9 Class 12 Maths Question 22.
\(\int _{ 0 }^{ \frac { 2 }{ 3 } }{ \frac { dx }{ 4+{ 9x }^{ 2 } } equals } \)
(a) \(\frac { \pi }{ 6 }\)
(b) \(\frac { \pi }{ 12 }\)
(c) \(\frac { \pi }{ 24 }\)
(d) \(\frac { \pi }{ 4 }\)
Solution:

Move to Top → Class 12 Integrals Chapter 7

Integration Class 12 Ex 7.10

Ex 7.10 Class 12 Maths Question 1:

Solution:

Ex 7.10 Class 12 Maths Question 2:

Solution:

Ex 7.10 Class 12 Maths Question 3:

Solution:

Ex 7.10 Class 12 Maths Question 4:

Solution:

Ex 7.10 Class 12 Maths Question 5:

Solution:


Ex 7.10 Class 12 Maths Question 6:

Solution:


Ex 7.10 Class 12 Maths Question 7:

Solution:

Ex 7.10 Class 12 Maths Question 8:

Solution:

Ex 7.10 Class 12 Maths Question 9:

Solution:

Ex 7.10 Class 12 Maths Question 10:

Solution:

Ex 7.10 Class 12 Maths Question 11:

Solution:




Ex 7.10 Class 12 Maths Question 12:

Solution:



Ex 7.10 Class 12 Maths Question 13:

Solution:

Ex 7.10 Class 12 Maths Question 14:

Solution:

Ex 7.10 Class 12 Maths Question 15:

Solution:

Ex 7.10 Class 12 Maths Question 16:

Solution:

Ex 7.10 Class 12 Maths Question 17:

Solution:


Ex 7.10 Class 12 Maths Question 18:

Solution:


Ex 7.10 Class 12 Maths Question 19:


Solution:

Ex 7.10 Class 12 Maths Question 20:


Solution:

Move to Top → Class 12 Integrals Chapter 7

NCERT Solutions for Class 2 Maths Integration Class 12 Ex 7.11

Move to Top → Class 12 Integrals Chapter 7

NCERT Solutions for Class 12 Maths Chapter 7 Integrals Miscellaneous Exercise

Miscellaneous Exercise Class 11 Maths Question 1:

Solution:

Miscellaneous Exercise Class 11 Maths Question 2:

Solution:

Miscellaneous Exercise Class 11 Maths Question 3:

Solution:

vMiscellaneous Exercise Class 11 Maths Question 4:

Solution:

Miscellaneous Exercise Class 11 Maths Question 5:

Solution:

Miscellaneous Exercise Class 11 Maths Question 6:

Solution:

Miscellaneous Exercise Class 11 Maths Question 7:

Solution:

Miscellaneous Exercise Class 11 Maths Question 8:

Solution:

Miscellaneous Exercise Class 11 Maths Question 9:

Solution:

Miscellaneous Exercise Class 11 Maths Question 10:

Solution:

Miscellaneous Exercise Class 11 Maths Question 11:

Solution:

Miscellaneous Exercise Class 11 Maths Question 12:

Solution:

Miscellaneous Exercise Class 11 Maths Question 13:

Solution:

Miscellaneous Exercise Class 11 Maths Question 14:

Solution:

Miscellaneous Exercise Class 11 Maths Question 15:

Solution:

Miscellaneous Exercise Class 11 Maths Question 16:

Solution:

Miscellaneous Exercise Class 11 Maths Question 17:

Solution:

Miscellaneous Exercise Class 11 Maths Question 18:

Solution:

Miscellaneous Exercise Class 11 Maths Question 20:

Solution:

Miscellaneous Exercise Class 11 Maths Question 21:

Solution:

Miscellaneous Exercise Class 11 Maths Question 22:

Solution:

Miscellaneous Exercise Class 11 Maths Question 23:

Solution:

Miscellaneous Exercise Class 11 Maths Question 24:

Solution:

Miscellaneous Exercise Class 11 Maths Question 25:

Solution:

Miscellaneous Exercise Class 11 Maths Question 26:

Solution:

Miscellaneous Exercise Class 11 Maths Question 27:

Solution:

Miscellaneous Exercise Class 11 Maths Question 28:

Solution:

Miscellaneous Exercise Class 11 Maths Question 29:

Solution:

Miscellaneous Exercise Class 11 Maths Question 30:

Miscellaneous Exercise Class 11 Maths Question 31:

Solution:

Miscellaneous Exercise Class 11 Maths Question 32:

Solution:

Miscellaneous Exercise Class 11 Maths Question 33:

Solution:

Miscellaneous Exercise Class 11 Maths Question 34:

Solution:

Question 35:

Solution:

Miscellaneous Exercise Class 11 Maths Question 36:

Solution:

Miscellaneous Exercise Class 11 Maths Question 37:

Solution:

Miscellaneous Exercise Class 11 Maths Question 38:

Solution:

Miscellaneous Exercise Class 11 Maths Question 39:

Solution:

Miscellaneous Exercise Class 11 Maths Question 40:

Solution:

Miscellaneous Exercise Class 11 Maths Question 41:

Solution:

Miscellaneous Exercise Class 11 Maths Question 42:

Solution:

Miscellaneous Exercise Class 11 Maths Question 43:

Solution:

Miscellaneous Exercise Class 11 Maths Question 44:

Solution:

Move to Top → Class 12 Integrals Chapter 7

Integration Formulas

गणित कक्षा 12 समाकलन प्रश्नावली 7.1

निम्नलिखित फलनों के प्रतिअवकलज ( समाकलन) निरीक्षण विधि द्वारा ज्ञात कीजिए।

Ex 7.1 Class 11 Maths प्रश्न 1.
sin 2x
हल-
∫sin 2x dx
हम जानते हैं कि, \(\frac { d }{ dx }\) cos2x = -2 sin 2x
या sin 2x = \(-\frac{1}{2} \frac{d}{d x}\)cos2x
sin 2x = \(\frac{d}{d x}\)(\(-\frac{1}{2}\)cos2x)
अतः sin 2x का प्रति अवकलज \(-\frac{1}{2}\)cos 2x है।

Ex 7.1 Class 11 Maths प्रश्न 2.
cos 3x
हल-
∫cos 3x dx
हम जानते हैं कि, \(\frac { d }{ dx }\) sin 3x = 3 cos 3x

अत: cos3x का प्रति अवकलज \(\frac{1}{3}\) sin 3x हैं।

Ex 7.1 Class 11 Maths प्रश्न 3.
e^2x
हल-
∫e^2x dx
हम जानते हैं कि,

Ex 7.1 Class 11 Maths प्रश्न 4.
(ax + b)²
हल-
∫(ax + b)² dx
हम जानते हैं कि,

Ex 7.1 Class 11 Maths प्रश्न 5.
sin 2x – 4e^3x
हल-
हम जानते हैं

निम्नलिखित समाकलनों को ज्ञात कीजिए।

Ex 7.1 Class 11 Maths प्रश्न 6.
∫(4e^3x + 1) dx
हल-
∫(4e^3x + 1) dx = 4∫e^3xdx + ∫1 dx

Ex 7.1 Class 11 Maths प्रश्न 7.

हल-

Ex 7.1 Class 11 Maths प्रश्न 8.
∫(ax² + bx + c) dx
हल-
∫(ax² + bx + c) dx = a∫x²dx + b∫xdx + c∫1 dx

Ex 7.1 Class 11 Maths प्रश्न 9.
∫(2x² + e^x) dx
हल-
∫(2x² + e^x) dx = 2∫x² dx + ∫e^x dx

Ex 7.1 Class 11 Maths प्रश्न 10.

हल-

Ex 7.1 Class 11 Maths प्रश्न 11.

हल-

Ex 7.1 Class 11 Maths प्रश्न 12.

हल-

Ex 7.1 Class 11 Maths प्रश्न 13.

हल-

Ex 7.1 Class 11 Maths प्रश्न 14.
∫(1-x)√x dx
हल-
∫(1-x)√x dx
=∫(√x-x√x)dx

Ex 7.1 Class 11 Maths प्रश्न 15.
∫√x(3x² + 2x + 3)dx
हल-
∫√x(3x² + 2x + 3)dx

Ex 7.1 Class 11 Maths प्रश्न 16.
∫(2x – 3cosx + e^x)dx
हल-
∫(2x – 3cosx + e^x)dx

प्रश्न 17.
∫(2x² – 3sinx + 5√x)dx
हल-
∫(2x² – 3sinx + 5√x)dx
= 2∫x² dx – 3 ∫ sinx dx + 5∫√x dx

Ex 7.1 Class 11 Maths प्रश्न 18.
∫secx (sec x + tan x) dx
हल-
∫sec x (sec x + tan x) dx
= ∫(sec² x + sec x tan x) dx
= ∫(sec² x dx
= ∫sec x tan x dx
tan x + sec x + C

Ex 7.1 Class 11 Maths प्रश्न 19.

हल-

Ex 7.1 Class 11 Maths प्रश्न 20.

हल-

प्रश्न 21 एवं 22 में सही उत्तर का चयन कीजिए

Ex 7.1 Class 11 Maths प्रश्न 21

हल-

Ex 7.1 Class 11 Maths प्रश्न 22

हल-