Binomial Theorem Notes Class 11 Maths Chapter 8

Binomial theorem for any positive integer
1. (a + b)ⁿ = ⁿC₀aⁿ + ⁿC₁a^n-1 + ⁿC₂a^n-2 + ………………..ⁿC_ra^n-rb^r + ………..+ ⁿC_nbⁿ

2. T_r+1 = general term = ⁿC_ra^n-rb^r … (1)
(a + b)ⁿ = \(\sum_{r=0}^{n}\)ⁿC_ra^n-rb^r

3. Some observations : (i) Number of terms in binomial expansion = Index of the binomial + 1 = n + 1.

(ii) In the successive terms of the expansion, the index of the first term is n and it goes on decreasing by unity. Thus, the indices of first term and n, n – 1, n – 2, …, 1, 0 while the index of second term starts from 0 and goes on increasing by 1. Therefore, the indices of second term are 0, 1, 2, … , n.

(iii) In any term of the expansion, the sum of indices of first term and second term is constant and it is equal to n.

(iv) Coefficients of these terms in the expansion are ⁿC₀, ⁿC₁, ⁿC_r. ……, ⁿC₂….., ⁿC_n

Note : These coefficients may also be denoted as
C (n, 0), C(n, 1), C (n, 2),…, C (n, r), …, C (n,n).

To find their values, we apply the formula

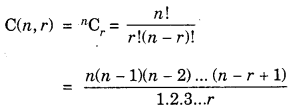
Whenever r > \(\frac{n}{2}\) , apply the formula
ⁿC_r = ⁿC_n-r
These coefficients may also be obtained with the help of Pascal’s triangles.

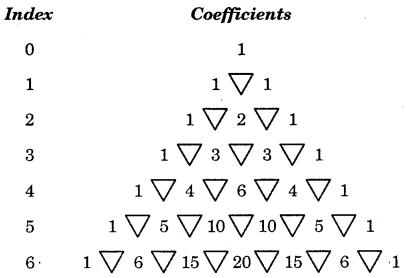
Now look at this pattern :
(a) First row; index 0; coefficient = 1.
(b) Second row; index 1; coefficients are 1, 1. A triangle is inserted between 1 and 1 as shown above.
(c) Third row; index 2; coefficients are 1, 2, 1.

Method : Two triangles, are drawn below each number of 1 of the second row. Adding 1 and 1 of second row we get 2 which is put below the third vertex of triangle. Write 1 each at the beginning arid end.

(d) Fourth row, index 3; coefficients are 1, 3, 3, 1. Method : Insert three triangles below 1, 2 and 1. 1 + 2 = 3 is written below the third vertex of first triangle, 2 + 1 = 3 is written below the second triangle.

Further, we proceed in the same manner.
(v) Coefficients ⁿC₀, ⁿC₁, ⁿC₂…, ⁿC_r, ⁿC_n in Binomial Theorem are known as Binomial Coefficients.

(vi) Replacing b by – b, in (1), we obtain
(a-b)ⁿ = ⁿC₀aⁿ – ⁿC₁a^n-1b + ⁿC₂a^n-2b² + ……….(-1)ⁿⁿC_ra^n-rb^r + ……….ⁿC_n(-b)ⁿ

(vii) Putting a = 1, b = x in (1), we obtain
(1+x)ⁿ = ⁿC₀ + ⁿC₁x + ⁿC₂x² + ……ⁿC_rx^r + …….. + ⁿC_nxⁿ

(viii) Putting a = 1, b = – x in (1), we obtain
(1-x)ⁿ = ⁿC₀ – ⁿC₁x + ⁿC₂x² – ….+ⁿC_r(-x)^r + …… + ⁿC_n(-x)ⁿ

(ix) Putting a = 1, b = 1 in (1), we obtain
(1+1)ⁿ = 2ⁿ = ⁿC₀ + ⁿC₁ + ⁿC₂ + ………..+ⁿC_n

(x) Putting a = 1, b = – 1, we obtain
0 = ⁿC₀ – ⁿC₁ + ⁿC₂ – ⁿC₃ + …..
or ⁿC₀ + ⁿC₂ + ⁿC₄ + ….. = ⁿC₁ + ⁿC₃ + …………+ ⁿC_r + ………

4. Middle Term : The expansion (a + b)n has n + 1 terms.
(i) If n + 1 is odd, the middle term is th = \(\frac{(n+1)+1}{2}\) th \(\frac{(n+2)}{2}\)th term.
(ii) If n + 1 is even, then
1st middle term = \(\frac{n+1}{2}\)th term
2nd middle term = \(\left(\frac{n+1}{2}+1\right)\)th term