CBSE Class 10 Maths Chapter 1 Notes Real Numbers
Real Numbers Class 10 Notes Understanding the Lesson
In class X, we have study about real numbers and encountered irrational numbers. In this chapter we want to know about natural numbers, whole numbers, integers, rational numbers, irrational numbers and real numbers.
1. Natural numbers: Natural numbers are those used for counting. e.g.: 1, 2, 3, 4, 5,… (and so on).
Natural numbers are denoted by N.
2. Whole numbers: Whole numbers are simply the numbers 0, 1, 2, 3, 4, 5,… (and so on).
Counting numbers are whole numbers. Without zero we cannot count. Whole numbers are denoted by W.
3. Integer: The set of integers consist of zero 0, the natural numbers and the negative of natural numbers.
e.g.: …-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … The integers are sometimes also called rational integers. Integers are denoted by Z. (Zahlen means to count)
4. Rational number: A rational number is any real number that can be expressed in the form \(\frac{p}{q} \)of R where q ≠ 0. Every integer is a rational number, the set of rational numbers is usually denoted by Q.
e.g : \(\frac{1}{2}, \frac{5}{1}, \frac{7}{9}\)
Note : The decimal expansion of rational number always either terminates after a finite number of digits, or they are non terminating and repeating decimals.
5. Irrational number: An irrational number is any real number that cannot be expressed as ratio of integers.
e.g : \(\sqrt{2}, \sqrt{3},\)π ,0.340440444…….. .These numbers cannot be represented as terminating or
repeating decimals.
6. Real number: The real number include all the rational numbers such as integers -5, -4, -1, 0, 1, 2,… and all fractions \(\frac{4}{3}, \frac{5}{11}, \ldots\) and all the irrational numbers such as \(\sqrt{2}, \sqrt{3}, \pi, \ldots\)
7. Algorithm: A set of rules for solving a problem in a finite number of steps.
8. Lemma: A lemma is a proven statement used for proving another statement.
9. Euclid Division Lemma: Euclid’s division lemma states that, for any two positive integers ‘o’ and ‘b’ there exists unique whole numbers q and r such that
a = bq + r, where 0 < r < b and a = dividend, b = divisor
q = quotient, r = remainder
i.e., Dividend = Divisor x Quotient + Remainder.
Euclid division lemma can be used to find the highest common factor (HCF) of any two positive integers.
9. Steps to obtain HCF using Euclid’s division lemma :
(i) Let us consider two positive integer a and b such that a >b.
Apply Euclid’s division lemma to the given integers a and b. Find two whole numbers q and r such that a = bq + r.
(ii) Now Check the value of r if r = 0 then b is the HCF of the given numbers. If r 0 then again apply Euclid’s division lemma to find the new divisor b and remainder r.
(iii) Continue the process till the remainder becomes zero. In that case the value of the divisor b is the HCF of a and b.
Note:
- HCF (a, b) = HCF (b, r)
- Euclid’s division algorithm can be extended for all integers except zero.
- Euclid’s division lemma and algorithm are so interlinked that people often call former as the division algorithm also.
10. Prime number: Any natural number which has exactly two factors is called prime number. e.g. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, … etc.
11. Composite number: A composite number is a positive integer that has at least one positive divisor other than one or the number itself.
OR
A composite number is any positive integer greater than one that is not a prime number. e.g.: 4, 6, 8, 9, 10, 12, 14, 15, 16,… etc.
12. Co-prime numbers: A set of numbers which do not have any common factor other than one are called co-prime numbers.
Note: Two numbers are said to be co-prime if their HCF is 1. e.g. 1. All prime numbers are co-prime to each other
13. Consecutive integers are always co-prime.
Statement of fundamental theorem of arithmetic : Every composite number can be expressed as a product of primes and this factorisation is unique apart from the order in which the prime factors occur.
Note:
- The prime factorisation of natural number is unique except for the order of its factors.
- HCF of two numbers is equal to the product of the terms containing least power of common prime factors of the two numbers.
- The LCM of two number is equal to the product of the terms containing the greatest power of all prime factors of the two numbers.
- For any two positive integers a and b HCF (a, b) x LCM (a,b) = a x b
- For any three positive numbers a, b and c
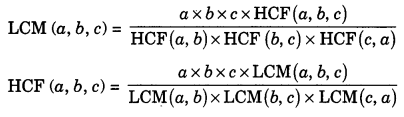
Revisiting Irrational Numbers: We have already studied irrational numbers and many of their properties. Now in this section, we will prove \(\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7} \)and in general, √P is irrational, where p is a prime.
(1) A number π is called irrational, if it can not be written in the form \(\frac{p}{q}\) where p and q are integers and q≠ 0. An irrational number is a real number that can not be written as simple fraction.
Theorem: Let p be a prime number. If p divides a2, then p divides a, where a is a positive integer.
Revisiting Rational Numbers and their Decimal Expansions
(1) Every rational number can be expressed as either terminating or non-terminating repeating decimal.
(2) Decimal expansion of every irrational number is non-terminating and non repeating.
(3) If the prime factorisation of denominator is of the form 2n x 5m where n and m are non-negative integers, then rational number will have terminating decimal expansion.
(4) Let x be a rational number whose decimal expansion terminates. Then x can be expressed in the form x=\(\frac{p}{q}\), where p and q are co-prime and the prime factorisation of q is of the form 2n x 5m where n and mare non-negative integers.
(5) Let x=\(\frac{p}{q}\) be a rational number, such that the prime factorisation of q is of the form 2n x 5m, where Q n, m are non-negative integers, then the decimal expansion of x terminates. e.g :\(\frac{3}{8}=\frac{3 \times 5^{3}}{2^{3} \times 5^{3}}=\frac{375}{10^{3}}=0.375\)
(6) Let x=\(\frac{p}{q}\) be a rational number, such that the prime factorisation of q is not of the form 2n x 5m , where n, m are non-negative integers, then x has a decimal expansion which is non-terminating (recurring) e.g : \( \frac{1}{7}=0 . \overline{142857}\)
Note: We conclude that decimal expansion of every rational number is either terminating or non-terminating recurring.