CBSE Class 9 Maths Chapter 5 Notes Triangles
Triangles Class 9 Notes Understanding the Lesson
Two geometric figures are said to be congruent if they have exactly the same shape and size.
Note: Congruent means equal in all respect. When one figure is kept over another then it should superimpose on the other to cover it exactly.
If a 500-rupee note is placed over another 500-rupee note then they cover each other.
If 5-rupee coin is placed over another 5-rupee coin of same year, then they cover each other completely.
Congruence of line segments: Two line segments are congruent if they are of the same length. Length of AB = length of CD
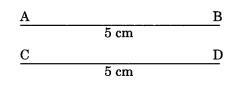
Hence, \(\overline{\mathrm{AB}} \cong \overline{\mathrm{CD}}\)
Congruence of angles: Two angles are congruent if they have equal degree measures.
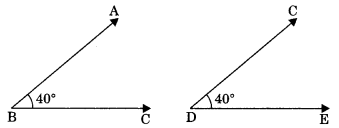
Hence, \(\angle \mathrm{ABC} \cong \angle \mathrm{CDE}\)
Congruence of squares: Two squares are said to be congruent, if they have equal sides.
Hence,
![]()
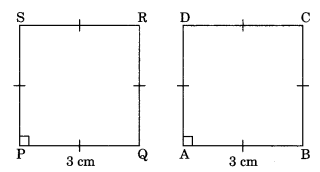
Note: Congruent plane figures are equal in area.
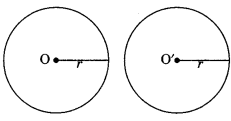
Congruence of circles: Two circles are congruent if they have equal radii.
Hence, Circle C1 ≅ Circle C2
Congruent Polygons
Two polygons are said to be congruent if they are the same size and shape. For existence of congruency,
(a) their corresponding angles are equal, and
(b) their corresponding sides are equal.
Congruence Triangles
Two triangles are congruent if they will have exactly the same three sides and three angles.
Axiom 7,1: SAS (Side-Angle-Side) Congruence rule: Two triangles are said to be congruent if two sides and the included angle of one triangle are equal to A D
the two sides and the included angle of the other.
In ΔABC and ΔDEF,
AB = DE
∠ABC = ∠DEF
BC = EF
ΔABC ≅ ΔDEF (by SAS)
Theorem 7.1: ASA (Angle-Side-Angle)
Congruence rule: Two triangles are said to be congruent, if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.
In Δ ABC and Δ DEF,
∠ABC = ∠DEF
BC = EF
∠ACB = ∠DFE
∴ΔABC = ΔDEF (by ASA)
Given: AABC and ADEF in which
∠ABC = ∠DEF, ∠ACB = ∠DFE and BC = EF
To Prove: ΔABC = ΔDEF
Proof: There are three cases arises for primary two congruence of the two triangles.
Case I: Let AB = DE
In ΔABC and ΔDEF,
AB = DE (assumed)
∠ABC = ∠DEF (given)
BC = EF (given)
So ΔABC ≅ ΔDEF (by SAS congruency)
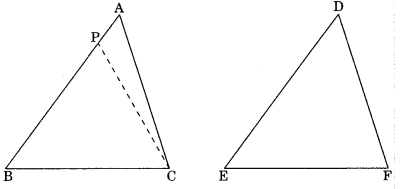
Case II: Let AB > DE. So we can take a point P on AB such that PB = DE.
Now in ΔPBC and ΔDEF
PB = DE (by construction)
∠PBC = ∠DEF (given)
BC = EF (given)
∴ ΔPBC ≅ ΔDEF (by SAS Congruency)
∠PCB = ∠DFE …(1) (by CPCT)
∴ ∠ACB = ∠DFE …(2)
From eqn (1) and (2),
∠PCB = ∠ACB
which is not possible. This is only possible if point P coincides with A.
Hence AB = DE (PB=AB)
So ΔABC = ΔDEF (by SAS congruency)
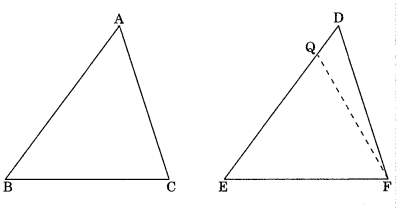
Case III: If AB < DE, so we take a point Q on DE such that QE = AB
Now in ΔABC and ΔQEF,
AB = QE (by construction)
∠ABC = ∠QEF (given)
BC = EF (given)
Hence ΔABC = ΔQEF (by SAS congruency)
∠ACB = ∠QFE (by CPCT)
But ∠ACB = ∠DFE
Hence ∠QFE = ∠DFE
which is only possible if point Q coincides with D.
∴ AB = DE
Hence ΔABC ≅ ΔDEF (by SAS congruency)
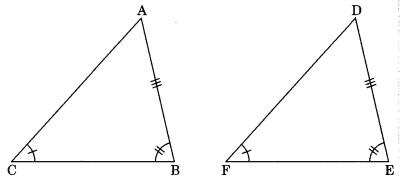
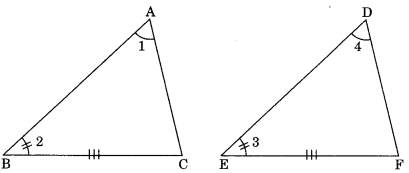
Corollary: AAS (Angle-Angle-Side) congruence rule:
Two triangles are said to be congruent if two angles and one side of one triangle is equal to two angles and one side of another triangle.
In A ABC and A DEF,
∠ACB = ∠DFE . ∠ABC – ∠DEF
AB = DE
∴ ΔABC = ΔDEF (by AAS)
Given: ΔABC and ΔDEF
In which ∠A = ∠D, ∠B = ∠E
and BC = EF
To Prove: ΔABC ≅ ΔDEF
Proof: In ΔABC and ΔDEF
∠1 = ∠4 … (1) (given)
and ∠2 = ∠3 … (2) (given)
Adding eqn. (1) and (2),
∠1 + ∠2 = ∠3 + ∠4
⇒ 180° – (∠1 + ∠2) = 180° – (∠3 + ∠4) (by angle sum property)
∠ACB = ∠DFE
Hence ΔABC ≅ ΔDEF
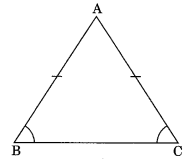
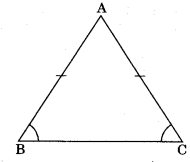
Theorem 7.2 Angle opposite to equal sides of an isosceles triangle are equal.
If AB = AC, then
∠ABC = ∠ACB
Given: ABC is a triangle in which
AB = AC
To Prove: ∠B = ∠C
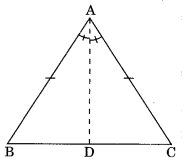
Construction:
Draw AD angle bisector of ∠A.
Proof: In ΔBAD and ΔCAD,
AB = AC (given)
∠BAD = ∠CAD (by construction)
AD = AD (common)
.∴ΔBAD = ΔCAD (by SAS)
Hence ∠B = ∠C (by CPCT)
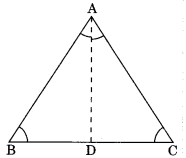
Theorem 7.3. The sides opposite to equal angles of a triangle are equal.
Given: ΔABC in which ∠B = ∠C
To Prove: AB = AC
Construction:
Draw AD bisector of ∠A which meets BC at D.
Proof: In ΔBAD and ΔCAD,
∠B = ∠C
∠BAD – ∠CAD
AD = AD
∴ΔBAD ≅ ΔCAD
Hence AB – AC
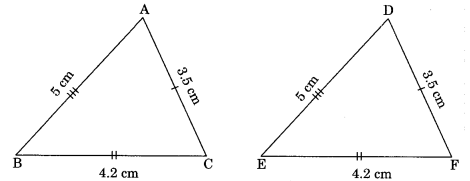
Theorem SSS (Side-Side-Side)
Congruence rule: Two triangles are said to be congruent if all sides (three) of one triangle are equal to the all sides (three sides) of another triangles then the two triangle are congruent.
In Δ ABC and Δ DEF,
AB = DF
BC = EF
AC = DE
ΔABC ≅ΔDEF
Theorem 7.5: RHS (Right angle-Hypotenuse-Side)
Congruence rule: If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of another triangle, their the two triangles are congruent.
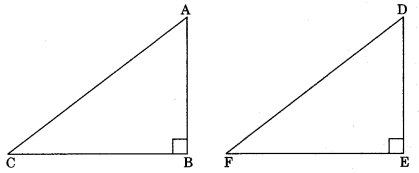
In ΔABC and ΔDEF,
∠ABC = ∠DEF
AC = DF
AB = DE
∴ ΔABC ≅ ΔDEF (by R.H.S)
Inequalities in a Triangle
Theorem 7.6: If two sides of a triangle are unequal, the angle opposite to the longer side is greater.
∠ABC > ∠BAC
∴ AC > BC
Given: ΔABC in which
AC > AB
To Prove:
∠ABC > ∠ACB
Construction:
Take a point D on AC such that AD = AB and join BD.
Proof: In Δ ABD,
AB – AD (by construction)
∴ ∠1 = ∠2 …(1) (Angle opposite to equal sides are equal)
∠2 > ∠3 ……..(2) ∠1 is exterior angle of ΔBCD)
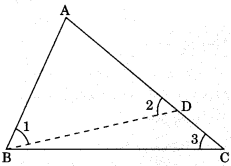
From eqn. (1) and (2),
∠1 > ∠3
Hence ∠ABC > ∠ACB.
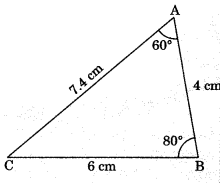
Theorem 7.7: In a triangle, side opposite to greater angle is longer.
If ∠ABC > ∠BAC
∴ AC > BC
Given: Δ ABC in which
∠ABC > ∠ACB
To Prove: AC > AB
Proof: Here three cases arises.
- AC = AB
- AC < AB
- AC < AC
Case I: If AC = AB
∠ABC – ∠ACB (Angle opposite to equal sides are equal)
But ∠ABC > ∠ACB (given)
This is a contradiction.
Hence AC ≠AB
∴ AC > AB
Case II: AC < AB
∠ACB > ∠ABC (Angle opposite to longer side is greater)
This is contradiction of given hypothesis.
Hence only one possibility is left.
i.e. AC > AB (It must be true)
Hence AC > AB
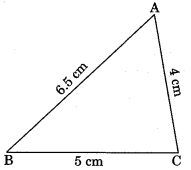
Theorem 7.8: The sum of any two sides of a triangle is greater than the third side.
(i) AB + AC > BC
(ii) AB + BC > AC
(iii) BC + AC > AB
Given: ΔABC
Prove that:
(i) AB + BC > AC
(ii) AB + AC > BC
(iii) AC + BC > BC
Construction: BA produce to D such that AD = AC. Join CD.
Proof: In ΔACD,
AC = AD (by construction)
∠2 = ∠1 (Angle opposite to equal sides are equal)
∠2 + ∠3 > ∠1 (∠2 + ∠3 = ∠BCD)
Hence ∠BCD > ∠BDC
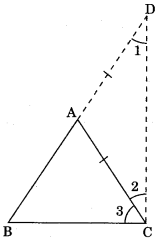
Hence BD > BC
⇒ AB + AC > BC (AD = AC by construction)
Similarly, AB + BC > AC
and AC + BC > AB
Median of a triangle: A line segment which joins the mid-point of the side to the opposite vertex. AD is median. D is the mid-point of BC.
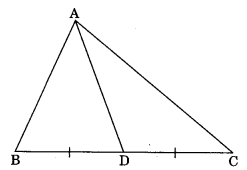
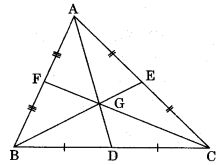
Centroid: The point of intersection of all three medians of a triangle is known as its centroid.
Note: Centroid G divides the medians in the ratio 2: 1, i.e., AG : GD = 2: 1
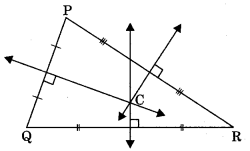
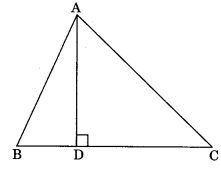
Altitude: Perpendicular drawn from a vertex to the opposite side.
Orthocentre: The point at which all the three altitudes intersect each other is known as orthocentre.
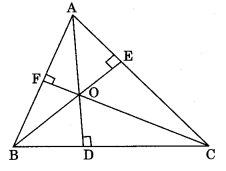
Incentre: The point at which the bisectors of internal angles of a triangle intersect each other is called incentre.
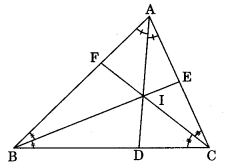
Circumcentre: The point at which perpendicular bisectors of the sides of a triangle intersect each other is called circumcentre.