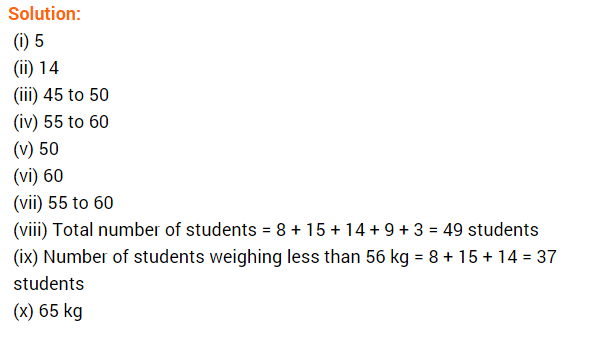Data Handling Class 8 Extra Questions Maths Chapter 5
Extra Questions for Class 8 Maths Chapter 5 Data Handling
Data Handling Class 8 Extra Questions Very Short Answer Type
Question 1.
In the class interval 5-10, find the
(i) lower limit
(ii) upper limit
(iii) class mark
(iv) class size
Solution:
(i) lower limit = 5
(ii) upper limit = 10
(iii) Class mark = \(\frac { 5+10 }{ 2 }\) = \(\frac { 15 }{ 2 }\) = 7.5
(iv) Class size = 10 – 5 = 5
Question 2.
A group of 20 students recorded their heights (in cm). The data received were as given below. What is the range?
150, 120, 112, 160, 155, 151, 158, 142, 148, 149, 161, 165, 140, 157, 156, 146, 148, 153, 138, 135
Solution:
The minimum height =112 cm
Maximum height = 165 cm
Range = Maximum height – Minimum height = 165 cm – 112 cm = 47 cm
Question 3.
In the given pie chart, which colour is most popular? Which colour is the least popular?

Solution:
Red colour is the most popular and the blue colour is the least popular.
Question 4.
A die is thrown once. Find the probability of getting a number greater than 4.
Solution:
Number greater than 4 = 5, 6
n(E) = 2
Sample space n(S) = 6
Probability of getting a number greater than 4
= \(\frac { n(E) }{ n(S}\) = \(\frac { 2 }{ 6 }\) = \(\frac { 1 }{ 3 }\)
Where re(E): Number of favourable outcomes
n(S): Total number of outcomes
Question 5.
A class consists of 21 boys and 9 girls. A student is to be selected for social work. Find the probability that
(i) a girl is selected
(ii) a boy is selected
Solution:
Sample space n(S) = 21 + 9 = 30
Number of girls n(E) = 9
(i) Probability of selecting a girl
= \(\frac { n(E) }{ n(S}\) = \(\frac { 9 }{ 30 }\) = \(\frac { 3 }{ 10 }\)
(ii) Probability of selecting a boy
= \(\frac { n(E) }{ n(S}\) = \(\frac { 21 }{ 30 }\) = \(\frac { 7 }{ 10 }\)
Question 6.
The following pie chart depicts the percentage of students, nationwide. What is the percentage of
(i) Indian students
(ii) African students?

Solution:
(i) Percentage of Indian students = \(\frac { 180\times 100 }{ 360 }\) = 50%
(ii) Percentage of African students = \(\frac { 45\times 100 }{ 360 }\) = 12\(\frac { 1 }{ 2 }\)%
Short Answer (SA) Questions
Question 7.
Fill in the blanks:

Solution:
Class-marks are
Class-mark


Question 8.
Construct a frequency table for the following marks obtained by 50 students using equal Intervals taking 16-24 (24 not included) as one of the class-intervals.
52, 16, 18, 20, 42, 48, 39, 38, 54, 58, 47, 37, 25, 16, 42, 49, 36, 35, 53, 21, 30, 43, 56, 34, 33, 17, 22, 24, 37, 41, 40, 50, 54, 56, 54, 36, 38, 42, 44, 56, 17, 18, 22, 24, 17, 48, 58, 23, 29, 58
Solution:

Question 9.
The double bar graph shows the average monthly temperatures of two cities over 4 months period. Read the graph carefully and answer the questions given below:
(i) What does each 1 cm block on the vertical axis represent?

(ii) What was the average monthly temperature in Dehradun in
(a) March
(b) April
(c) May
(d) June?
(iii) What was the average monthly temperature in Delhi for the whole 4 months?
(iv) In which month was the difference between the temperature of Delhi and Dehradun maximum and how much?
Solution:
(i) 1 cm block on vertical axis = 10°C
(ii) The average monthly temperature in Dehradun in the month of
(a) March was 25°C
(b) April was 34°C
(c) May was 40°C
(d) June was 36°C
(iii) The average monthly temperature in Delhi in the 4 months

(iv) Difference between the average monthly temperature of Delhi and Dehradun was maximum in the month of June, i.e. (50° – 36°) = 14°C.
Question 10.
The following table represents the number of students in a school playing six different games.

Present the above information on a bar graph.
Solution:

Question 11.
Prepare a grouped frequency table for the given histogram.

Solution:

Question 12.
A bag contains 144 coloured balls represented by the following table. Draw a pie chart to show this information.

Solution:

Question 13.
Mrs Verma spends her allowance in the following way.

Represent the above information by a pie chart.
Solution:


Question 14.
What is the probability of getting a marble which is not red from a bag containing 3 black, 8 yellow, 2 red and 5 white marbles?
Solution:
Total number of balls = 3 black + 8 yellow + 2 red + 5 white = 18
n( S) = 18
Number of the balls which are not red = 3 + 8 + 5 = 16
n(E) = 16
Probability = \(\frac { n(E) }{ n(S) }\) = \(\frac { 16 }{ 18 }\) = \(\frac { 8 }{ 9 }\)
Question 15.
From a well shuffled deck of 52 playing cards, a card is selected at random. Find the probability of getting
(i) a black card
(ii) a black king
(iii) an ace
(iv) a card of diamond
Solution:
Here, n(S) = 52
(i) Total number of black card = 26
n(E) = 26
Probability of getting a black card = \(\frac { n(E) }{ n(S) }\) = \(\frac { 26 }{ 52 }\) = \(\frac { 1 }{ 2 }\)
(ii) Number of black king = 2
n(E) = 2
Probability of getting a black king = \(\frac { n(E) }{ n(S) }\) = \(\frac { 2 }{ 52 }\) = \(\frac { 1 }{ 26 }\)
(iii) Number of aces = 4
n(E) = 4
Probability of getting an ace = \(\frac { n(E) }{ n(S) }\) = \(\frac { 4 }{ 52 }\) = \(\frac { 1 }{ 13 }\)
(iv) Number of diamond cards = 13
n(E) = 13
Probability of getting a card of diamond = \(\frac { n(E) }{ n(S) }\) = \(\frac { 13 }{ 52 }\) = \(\frac { 1 }{ 4 }\)