Co-ordinates of a Point: The co-ordinates of a point are the distances from the origin of the feet of the perpendiculars from the point on the respective co-ordinate axes.

Distance Formula : The distance between the points (x₁ y₁, z₁) and (x₂, y₂, z₂) is given by \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\). The distance of the point (x, y, z) from the origin is given by \(\sqrt{x^{2}+y^{2}+z^{2}}\)

Section Formulae: .
(i) Section formula for internal division :
If P(x₁ y₁, z₁) and Q(x₂, y₂, z₂) are two points. Let R be a point on the line segment P and Q such that it divides the join of P and Q internally in the ratio m₁ : m₂.

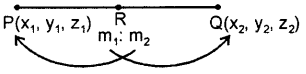
Then, the co-ordinates of R are

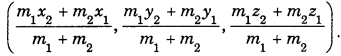
(ii) Section formula for external division :
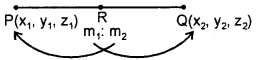
If P(x₁ y₁, z₁) and Q(x₂, y₂, z₂) are two points and let R be a
point on PQ produced dividing it
externally in the ratio m₁ : m₂(m₁ ≠ m₂). Then, the co-ordinates of Rare

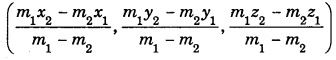
Mid-Point : The mid-point of the line segment joining (x₁ y₁, z₁) and (x₂ y₂, z₂) is \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}, \frac{z_{1}+z_{2}}{2}\right)\)

Centroid : Centroid of the triangle whose vertices are (x₁ y₁, z₁), (x₂ y₂, z₂) and (x₃ y₃, z₃) is