Left Hand Limit: The \(\lim _{x \rightarrow a^{-}}\)f(x) is the expected value f(x) at x = a, given the values of fix) near x to the left of a. This value is called the left hand limit of f(x) at a.

Right Hand Limit : The \(\lim _{x \rightarrow a^{+}}\)f(x) is the expected value of f(x) at x – a, given the values of fix) near x to the right of a. ‘ ‘his value is called the right hand limit of f(x) at a.

Limit of a Function: If the right and left hand limits coincide, the common value of the limit of f(x) as x → a is called the limit of a function. It is denoted by \(\lim _{x \rightarrow a}\)f(x).

Algebra of Limits:
(i) Limit of sum of two functions is sum of the limits of the functions, i.e.,
\(\lim _{x \rightarrow a}\) [(x)+g(x)] = \(\lim _{x \rightarrow a}\)f(x) + \(\lim _{x \rightarrow a}\) g(x).

(ii) Limit of difference of two functions is difference of the limits of the functions, i.e.,
\(\lim _{x \rightarrow a}\) [(x)-g(x)] = \(\lim _{x \rightarrow a}\)f(x) – \(\lim _{x \rightarrow a}\) g(x).

(iii) Limit of product of two functions is product of the limits
of the functions i.e.,
\(\lim _{x \rightarrow a}\) [(x)+g(x)] . \(\lim _{x \rightarrow a}\)f(x) . \(\lim _{x \rightarrow a}\) g(x).

(iv) Limit of quotient of two functions is quotient of the limits of the functions (whenever the denominator is non-zero i.e..
\(\lim _{c \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}\)

(v) \(\lim _{x \rightarrow a}\) (c.f)(x) = c\(\lim _{x \rightarrow a}\)f(x)

Limit of Polynomial:
Let f(x) = a₀ + a₁x + a + a₂x² + … + a_nxⁿ be a polynomial function.
Let \(\lim _{x \rightarrow a}\) x^k = a^k.
\(\lim _{x \rightarrow a}\) f(x) = [a₀ + a₁x + a + a₂x² + … + a_nxⁿ]
= a₀ + a₁\(\lim _{x \rightarrow a}\)x + a + a₂\(\lim _{x \rightarrow a}\)x² + … + a_n\(\lim _{x \rightarrow a}\)xⁿ
= a₀ + x₁a + a₂a² + … + a_naⁿ
= f(a).

Limit of Rational Function : A function f is said to be a rational function, if f(x) = \(\frac{g(x)}{h(x)}\), where g(x) and h(x) are polynomials h(x) ≠ 0

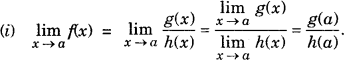
However, ifg(a) = 0 and h(a) = 0, i.e., this is of the form 0/0 then factor(s),x-a of g(x) and h(x) are determined and then cancelled out.
Let g(x) = (x-a)p(x)
h(x) = (x-a)q(x)

(ii) For any positive integer n,
\(\lim _{x \rightarrow a} \frac{x^{n}-a^{n}}{x-a}\) = na^n-1

Theorems:
(i) Let f and g be two real valued functions with the same domain such that f(x) ≤ g(x) for allx in the domain of definition. For some a, if both \(\lim _{x \rightarrow a}\)f(x) and \(\lim _{x \rightarrow a} g(x) exist, then
\lim _{x \rightarrow a}f(x) ≤ \lim _{x \rightarrow a}\)g(x)

(ii) Sandwich Theorem : Let f, g and h be real functions
such that f(x) ≤ g(x) ≤ h(x) for all x in the common domain of
definition. For some real number a, if \(\lim _{x \rightarrow a}\)g(x) f(x) = Z, \(\lim _{x \rightarrow a}\)g(x) = h(x) = l, then lim g(x) = l.

Limit of Trigonometric Functions :
(i) \(\lim _{x \rightarrow 0} \frac{\sin x}{x}\) = 1
(ii) \(\lim _{x \rightarrow 0} \frac{1-\cos x}{x}\) = 0

Derivative of f(x) at x = a : Suppose f is a real valued of function and a is a point in its domain of definition. The derivative of f at x = a is defined by
\(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\)
provided this limit exists. It is denoted by f'(a).

Derivative of fix) : Suppose f is a real valued function, the function defined by \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) wherever the limit exists is defined to be the derivative of/‘and is denoted by fix). Thus,

f ‘(x) = \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

Algebra of Derivative of Functions:
(i) Derivative of sum of two functions is sum of the derivatives of functions:
\(\frac{d}{d x}\)[f(x) + g(x)] = [\(\frac{d}{d x}\)f(x) + \(\frac{d}{d x}\)g(x)]
or (u + v)’ = u’ + v’.

iii) Derivative of difference of two functions is the difference of the derivatives of the functions :
\(\frac{d}{d x}\)[f(x) – g(x)] = [\(\frac{d}{d x}\)f(x) – \(\frac{d}{d x}\)g(x)]
or (u + v)’ = u’ + v’.

(iii) Derivative of product of two functions is given by the product rule, i.e.,
or (u .v)’ = u’v + uv’.

(iv) Derivative of quotient of two functions is given by quotient rule (whenever the denominator is non-zero).

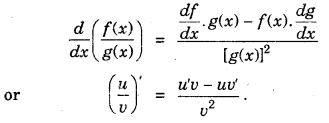
(v) Derivative of λf(x)
\(\frac{d}{d x}\)[λf(x)] = λ \(\frac{d y}{d x}\)f(x)
or (λu)’ = λu’

Some Derivatives:
(i) \(\frac{d}{d x}\)xⁿ = nxn-1
(ii) \(\frac{d}{d x}\)(ax + b)ⁿ = na(ax + b)^n-1
(iii) If f(x) = a₀xⁿ + a₁x^n-1 + a₂x^n-2 + … a_m
then na₀x^n-1 + (n-1)a₁x^n-2 + (n-2)a₂x^n-3+ …….. +a_n-1
(iv) \(\frac{d}{d x}\) (sin x) = cos x.
(v) \(\frac{d}{d x}\) (cos x) = – sin x.
(vi) \(\frac{d}{d x}\) (tan x) = sec² x.
(vii) \(\frac{d}{d x}\) (cosec x) = – cosec x cot x.
(viii) \(\frac{d}{d x}\) (sec x) = sec x tan x.
(ix) \(\frac{d}{d x}\) (cot x) = cosec² x