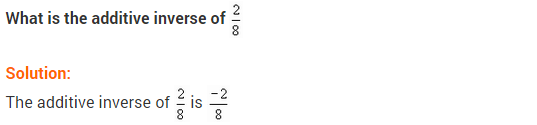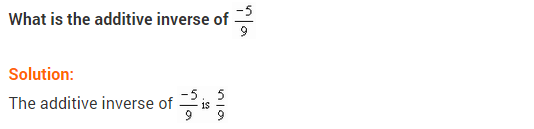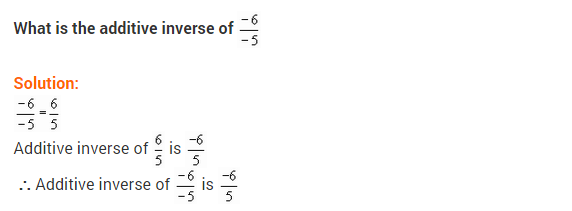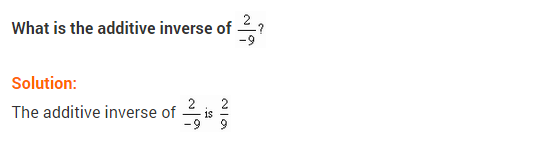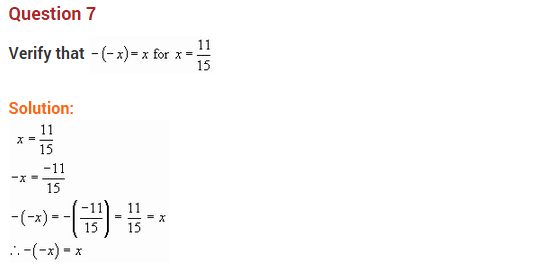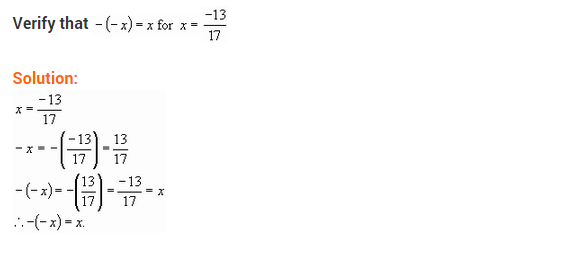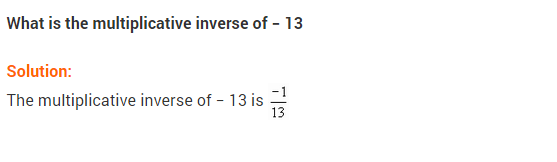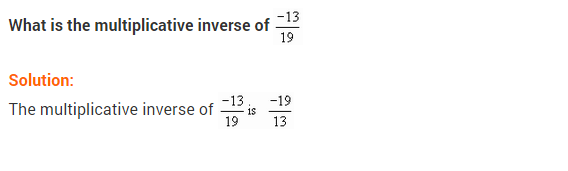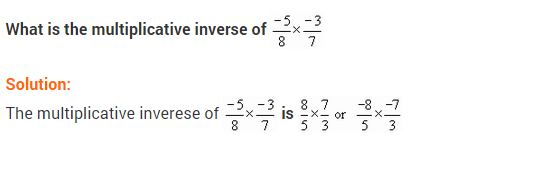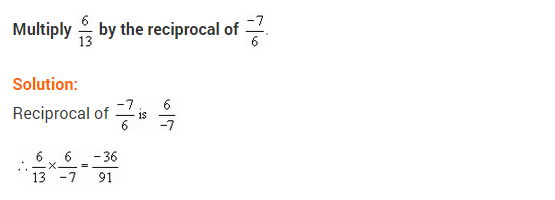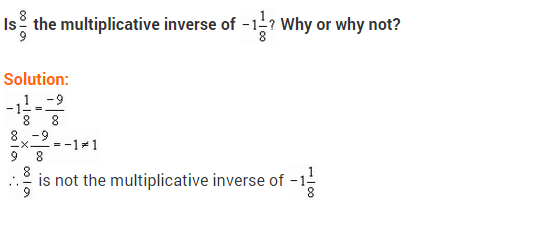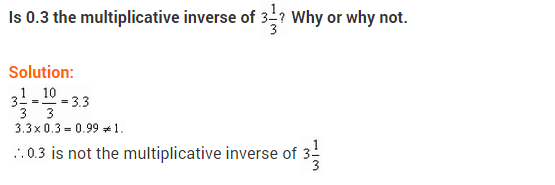NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Exercise 1.1
NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Exercise 1.1
Ex 1.1 Class 8 Maths Question 1.
Using appropriate properties find:
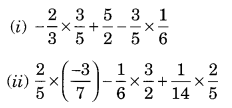
Solution:


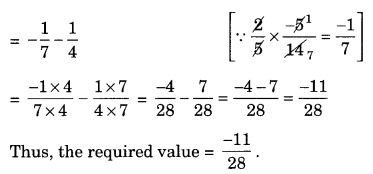
Ex 1.1 Class 8 Maths Question 2.
Write the additive inverse of each of the following:
(i) \(\frac { 2 }{ 8 }\)
(ii) \(\frac { -5 }{ 9 }\)
(iii) \(\frac { -6 }{ -5 }\)
(iv) \(\frac { 2 }{ -9 }\)
(v) \(\frac { 19 }{ -6 }\)
Solution:

Ex 1.1 Class 8 Maths Question 3.
Verify that -(-x) = x for
(i) x = \(\frac { 11 }{ 5 }\)
(ii) x = \(\frac { -13 }{ 17 }\)
Solution:
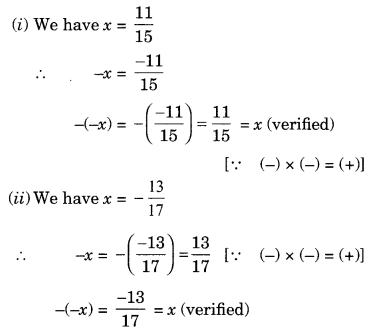
Ex 1.1 Class 8 Maths Question 4.
Find the multiplicative inverse of the following:
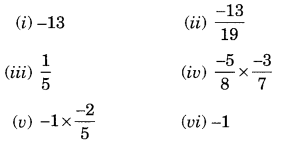
Solution:
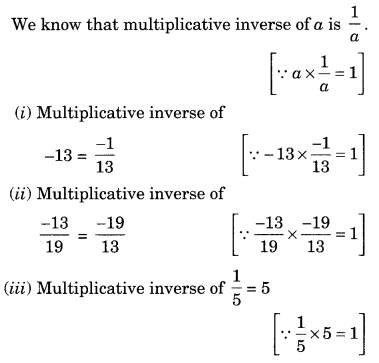

Ex 1.1 Class 8 Maths Question 5.
Name the property under multiplication used in each of the following:
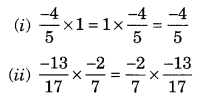
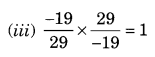
Solution:
(i) Commutative property of multiplication
(ii) Commutative property of multiplication
(iii) Multiplicative inverse property
Ex 1.1 Class 8 Maths Question 6.
Multiply \(\frac { 6 }{ 13 }\) by the reciprocal of \(\frac { -7 }{ 16 }\).
Solution:
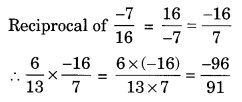
Ex 1.1 Class 8 Maths Question 7.
Tell what property allows you to compute
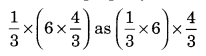
Solution:
Since a × (b × c) = (a × b) × c shows the associative property of multiplications.
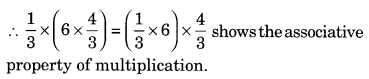
Ex 1.1 Class 8 Maths Question 8.
Is \(\frac { 8 }{ 9 }\) the multiplicative inverse of -1\(\frac { 1 }{ 8 }\)? Why or Why not?
Solution:
Here -1\(\frac { 1 }{ 8 }\) = \(\frac { -9 }{ 8 }\).
Since multiplicative inverse of \(\frac { 8 }{ 9 }\) is \(\frac { 9 }{ 8 }\) but not \(\frac { -9 }{ 8 }\)
\(\frac { 8 }{ 9 }\) is not the multiplicative inverse of -1\(\frac { 1 }{ 8 }\)
Ex 1.1 Class 8 Maths Question 9.
If 0.3 the multiplicative inverse of 3\(\frac { 1 }{ 3 }\)? Why or why not?
Solution:
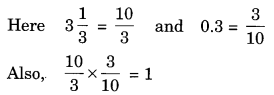
Multiplicative inverse of 0.3 or \(\frac { 3 }{ 10 }\) is \(\frac { 10 }{ 3 }\).
Thus, 0.3 is the multiplicative inverse of 3\(\frac { 1 }{ 3 }\).
Ex 1.1 Class 8 Maths Question 10.
Write:
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Solution:
(i) 0 is the rational number which does not have its reciprocal
[∵ \(\frac { 1 }{ 0 }\) is not defined]
(ii) Reciprocal of 1 = \(\frac { 1 }{ 1 }\) = 1
Reciprocal of -1 = \(\frac { 1 }{ -1 }\) = -1
Thus, 1 and -1 are the required rational numbers.
(iii) 0 is the rational number which is equal to its negative.
Ex 1.1 Class 8 Maths Question 11.
Fill in the blanks.
(i) Zero has ……….. reciprocal.
(ii) The numbers ……….. and ……….. are their own reciprocals.
(iii) The reciprocal of -5 is ………
(iv) Reciprocal of \(\frac { 1 }{ x }\), where x ≠ 0 is ……….
(v) The product of two rational numbers is always a …………
(vi) The reciprocal of a positive rational number is ……….
Solution:
(i) no
(ii) -1 and 1
(iii) \(\frac { -1 }{ 5 }\)
(iv) x
(v) rational number
(vi) positive