Trigonometric Functions Class 11 Notes Maths Chapter 3
Important Definitions:
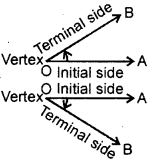
Angle: An angle is considered as a figure obtained by rotating a given ray about its initial point. The original position of the ray is called the initial side and the final position is called the terminal side of the angle. The point of rotation is called the vertex.
Positive Angle : If the direction of the rotation is anticlockwise, the angle is said to be positive.
Negative Angle : If the direction of the rotation is clockwise, the angle is said to be negative.
Degree measure of an angle: If a rotation from initial side of the terminal side is (\(\frac{1}{360}\))th of a revolution, the angle is said to have a measure of one degree, written as 1°.
1° = 60′ [One degree = 60 minutes]
1′ = 60″ [One minute = 60 seconds]
Radian Measure : An angle with its vertex at the centre of a circle which intercepts an arc equal in length to the radius of the circle is said to have a measure of 1 radian.
Important Formulae:
- θ = \(\frac{l}{r}\)
where θ = angle subtended by arc of length l at the centre of the circle and
r = radius of the circle. - π radians = 180°.
- 1 radian = \(\left(\frac{180}{\pi}\right)^{\circ}\)
- 1° = radian = 0.01746 (app.)
Circular Functions: Let a circle of unit radius be drawn with centre O. A line segment OP = 1 is rotated from the initial position OX, in the anticlockwise direction.
Let OP makes an angle θ with OX. The x-coordinate of P gives the value of cos θ and y – coordinate will give the value of sin θ. P may be any where on the circle and hence θ may acquire any value from 0 to 2π radians. Thus, we get the value of cos θ and sin θ for any value of θ.
These trigonometric functions are known as circular functions.
Important Formulae :
- sin2 θ – co2 θ = 1
- 1 + tan2 θ = sec2 θ
- 1 + cot2 θ = cosec2 θ
Periodic Functions : A function f is said to be periodic, if there exists a real number T > 0 such that f(x + T) = f(x) for all values of x. Then, T is called the period of the function.
Trigonometric actions are also periodic.
Here, cos (2nπ + x) = cos x
sin (2 nn + x) = sin x
Trigonometric Ratios (T-Ratios) Of Angle (-x)
- sin(-x) = -sin x,
- cos (- x) = cos x,
- tan (-x) = -tan x,
- cosec (- x) = – cosec x,
- sec(-x) = sec x,
- cot (- x) = – cot x.
T-Ratios of (\(\frac{\pi}{2}\) – x)
- sin (\(\frac{\pi}{2}\)-x) = cos x
- cosec (\(\frac{\pi}{2}\)-x) = sec x
- cos (\(\frac{\pi}{2}\)-x) = sin x
- tan (\(\frac{\pi}{2}\)-x) = cot x
- sec (\(\frac{\pi}{2}\)-x) = cosec x
- cot (\(\frac{\pi}{2}\)-x) = tan x
T-Ratios of (\(\frac{\pi}{2}\) + x)
- sin (\(\frac{\pi}{2}\)-x) = cos x
- cos (\(\frac{\pi}{2}\)-x) = -sin x
- tan (\(\frac{\pi}{2}\)-x) = -cot x
- cosec (\(\frac{\pi}{2}\)-x) = sec x
- sec (\(\frac{\pi}{2}\)-x) = -cosec x
- cot (\(\frac{\pi}{2}\)-x) = -tan x
T-Ratios of (π -x)
- sin (π – x) = sin x,
- cos (π – x) = – cos x,
- tan (π – x) = – tan x,
- cosec (π – x) = cosec x,
- sec (π – x) = – sec x,
- cot (π – x) = – cot x.
T-Ratios of (π+ x)
- sin (π + x) = – sin x,
- cos (π + x) = – cos x,
- tan (π + x) = tan x,
- cosec (π + x) = – cosec x,
- sec (π + x) = – sec x,
- cot (π + x) = cot x.
T-Ratios of (2π – x)
- sin (2π – x) = – sin x,
- cos (2n – x) = cos x,
- tan (2π – x) = – tan x,
- cosec (2π – x) = – cosec x,
- sec (2π – x) = sec x,
- cot (2π -x) = – cot x.
T-Ratios of (2π + x)
- sin (2π + x) = sin x,
- cos (2π + x) = cos x,
- tan (2π + x) = tan x,
- cosec (2π + x) = cosec x,
- sec (2π + x) = sec x,
- cot (2π+x)=cotx.
Note : To learn these formulae by heart, we adopt the following method :
I. First of all, we determine the sign of t-ratio under consideration.
The phrase Add Sugar To Coffee is quite helpful. We write Add, Sugar, To,
Coffee in I, II, III, IV quadrants respectively.
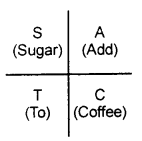
- The letter A of word ‘add’ indicates all the f-ratios of angles lying in the first quadrant are positive.
- The letter S of word ‘sugar’ indicates sin and cosec of the angle lying in II quadrant are positive and rest of t-ratios are negative.
- T of word ‘to’ indicates tan and cot of the angle lying in the third quadrant are positive and rest of the t-ratios of such angles are negative.
- C of the word coffee shows that cos and sec of the angles lying in IV quadrant are positive and rest of t-ratios are negative of such angles.
II. (i) For -angle – x, π – x, π + x, 2π – x, 2π + x, the t-ratios remains to be the same.
sin (- x) = – sin x, tan (π + x) = tan x, cos (2π -x) = cos x.
(ii) For angles \(\frac{\pi}{2}\) – x, \(\frac{\pi}{2}\) + x, \(\frac{3\pi}{2}\) – x, \(\frac{3\pi}{2}\)+ x the t-ratio changes from cos to sin , tan to cot and sec to cosec and vice versa.
e.g., sin(\(\frac{\pi}{2}\) + x) = cosx, tan(\(\frac{\pi}{2}\) – x) = cot x,
sec(\(\frac{\pi}{2}\) + x) = -cosec x etc.
T-Ratios of (x + y)
- sin (x + y) = sin x cos y + cos x sin y
- cos (x + y) = cos x cos y – sin x sin y
- tan (x + y) = \(\frac{\tan x+\tan y}{1-\tan x \tan y}\)
- cot(x + y) = \(\frac{\cot x \cot y-1}{\cot x+\cot y}\)
T-Ratios of (x – y)
- sin Or – y) = sin x cos y – cos x- sin y
- cos (x -y) = cos x cos y + sin x sin y
- tan(x – y) = \(\frac{\tan x-\tan y}{1+\tan x \tan y}\)
- cot(x – y) = \(\frac{\cot x \cot y+1}{\cot y-\cot x}\)
T-Ratios of (2x)
- sin 2x = 2sin x cos x = \(\frac{2 \tan x}{1+\tan ^{2} x}\)
- cos 2x = cos2 x – sin2 x = 2cos2 x – 1 = 1 – 2sin2 x
= \(\frac{1-\tan ^{2} x}{1+\tan ^{2} x}\) - tan 2x = \(\frac{2 \tan x}{1-\tan ^{2} x}\)
T-Ratios of (3x)
- sin 3x = 3sin x – 4sin3 x.
- cos 3x = 4cos3 x – 3 cos x.
- tan3 x = \(\frac{3 \tan x-\tan ^{3} x}{1-3 \tan ^{2} x}\)
Sum and Difference of two like ratios :
- sm x + sin y = 2sin\(\frac{x+y}{2}\) cos \(\frac{x-y}{2}\)
- sin x – sin y = 2cos \(\frac{x+y}{2}\) sin \(\frac{x-y}{2}\)
- cos x + cos y = 2cos \(\frac{x+y}{2}\) cos\(\frac{x-y}{2}\)
- cos x – cos y = – 2sin\(\frac{x+y}{2}\) sin\(\frac{x-y}{2}\)
Product of T-Ratios:
- 2 sin x cos y = sin (x + y) + sin (x – y).
- 2 cos x sin y = sin (x + y) – sin (x – y).
- 2 cos x cos y = cos (x + y) + cos (x – y).
- 2 sin x sin y = cos (x – y) – cos (x + y).
General solution of an equation :
- If sin x = 0, then x = nπ, n ∈ Z.
- If cos x = 0, then x = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z.
- If tan x = 0, then x = nπ, n ∈ Z.
- sin x = sin y ⇒ x = nπ + (- 1 )ny, n ∈ Z.
- cos x = cos y ⇒ x = 2nπ ±y, n ∈ Z.
- tan x = tan y ⇒ x = nπ+y, n ∈ Z,
where y is the principal value of x.