CBSE Class 9 Maths Chapter 8 Notes Linear Equations in Two Variables
Linear Equations in Two Variables Class 9 Notes Understanding the Lesson
1. Equation: An equation is a mathematical statement that two things are equal. It consists of two expressions one on each side of an equals sign. For example,7x + 9 = 0
2. An equation in a statement of an equality containing one or more variables.
7x + 3y = 10
3. Linear equation in one variable: A linear equation or first degree equation, in the single variable x is an equation that can be written in the form ax + b = 0 where a, and b are equal numbers, when a≠0.
Examples:
- 2x+3=0
- 3y + 4 = \(\frac{y}{3}\)
- 7x-\(\frac{9}{2}\) =0
- 3x -7y = 73
These equations are solved by applying the properties of real numbers and properties of equality.
4. Solution of a linear equation: The value of the variable which when substituted in place of variable makes both sides of the given equation equal, is called the solution of given equation. These values of variables is also known as root of the equation.
Example:
3x + 4y – 5
Let x – 3, and y = -1
Putting x- 3 and y = -1 in the given equation 3 x 3 + 4 x (-1) = 5
⇒ 9 – 4 = 5
⇒ 5 = 5
∴ LHS = RHS
Hence (3, -1) is a solution of given equation.
5. Linear equation in two variables: A linear equation in two variables is a first degree equation which can be written in the form ax + by + c – 0 and a, b both are non-zero real number. Where a, b and c are real numbers.
Examples:
- 3x + 2y – 9 = 0
- 7x – 4y + 6 = 0
6. Graph of a Linear Equation in two Variables
Graph of a linear equation in two variables is a straight line.
Steps of graphing a line
- If the equation is not in slope intercept form, i.e., y = mx + c, then write the equation in such form.
- Plot they intercept at (0, 6).
- Plot two or three more points by counting the rise and run from the y intercepts.
While solving the equation we should put the following points in our mind. •
- We should add or subtract the same number on both the sides of the equation.
- We should multiply or divide by the same non-zero real number on both sides of the equation.
Note:
- A linear equation in one variable has only one solution.
- A linear equation in two variables has infinitely many solutions.
(a) If the slope is positive, count upward for the rise and to the right for the run (also down and left)
Example; y = \(\frac{2}{3}\) x + 1
(b) If the slope is negative, count downward for the rise and to the right for the run (also up and left) Example: y =\(\frac{2}{3} \)x + 1
7. Draw a line through the points and place arrows on the ends. Extend the line to cover the whole grid (not just connect the two points)
Note:
- The graph of every first degree equation in two variables is a straight line.
- Equation of x-axis is y = 0 (:Hi) Equation of y-axis is x = 0
- The graph of x = a is a straight line parallel to y-axis.
- The graph of y = b is a straight line parallel to x-axis.
- Graph of the equation y = mx (i.e., has no intercepts) is a straight line passing through origin.
Every point which lies on the graph of the linear equation in two variables is a solution of linear equation. - Graph of linear equation in one variable
- If given equation is in variable x only then its value represented graphically is on x-axis.
- If the given equation is in variable y only then its value represented graphically is on y-axis.
8. Graph of linear equation in one variable
- If given equation is in variable x only then its value represented graphically is on x-axis.
- If the given equation is in variable y only then its value represented graphically is on y-axis.
For example, 2x = 5 ⇒ x=\(\frac{5}{2}\)
Representation: In one variable,

In Cartesian plane or in two variables,
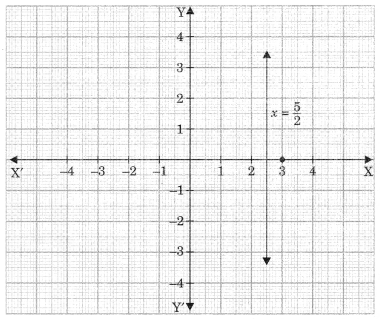
Draw a line through \(x=\frac{5}{2}\) parallel to y-axis. In such representation, the equation has many solutions.