CBSE Class 9 Maths Chapter 9 Notes Quadrilaterals
Quadrilaterals Class 9 Notes Understanding the Lesson
Quadrilateral
A plane figure bounded by four line segments is called quadrilateral.
Properties:
- It has four sides.
- It has four vertices or comers.
- It has two diagonals.
- The sum of four interior angles is equal to 360°.
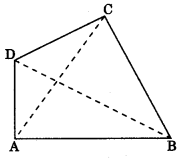
In quadrilateral ABCD, AB, BC, CD and DA are sides; AC and BD are diagonals and
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.
Types of Quadrilaterals
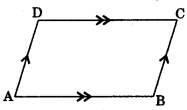
1. Parallelogram: A quadrilateral whose each pair of opposite sides are parallel.
- AB || DC
- AD || BC
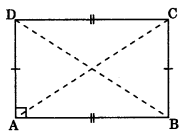
2. Rectangle: A parallelogram whose one angle is 90°. Diagonals are equal.
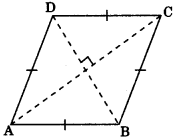
3. Rhombus: A parallelogram whose adjacent sides are equal.
Note: Diagonal bisect each other at 90°.
4. Square: A rectangle whose adjacent sides are equal (four sides are equal). Diagonal bisect each other at 90°.
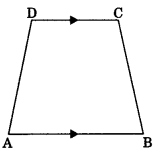
5. Trapezium: A quadrilateral whose one pair of opposite sides are parallel. AB || DC
6. Kite: It has two pair of adjacent sides that are equal in length but opposite sides are unequal.
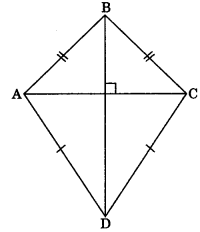
Note:
- One of the diagonal bisects the other at right angle.
- One pair of opposite angles are equal.
Properties of a Parallelogram
- Opposite sides are equal.
e.g., AB = DC and AD = BC - Consecutive angles are supplementary.
e.g., ∠A + ∠D = 180° - Diagonals of parallelogram bisect each other.
- Diagonal divide it into two congruent triangles. A B
Theorem 8.1: A diagonal of a parallelogram divides it into two congruent triangles.
Theorem 8,2: In a parallelogram, opposite sides are equal.
Theorem 8.3: If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Theorem 8.4: In a parallelogram, opposite angles are equal.
Theorem 8.5: If in a quadrilateral, each pair of opposite angles of a quadrilateral is equal then it is a parallelogram.
Theorem 8.6: The diagonals of a parallelogram bisect each other.
Theorem 8.7: If the diagonals of quadrilateral bisect each other, then it is a parallelogram.
Theorem 8.8: A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.
Mid-point Theorem
Theorem 8.9: The line segment joining the mid-points of two sides of a triangle is parallel to the third.
Given: A triangle ABC, E and F are mid-points of sides AB and AC respectively.
i.e., AE = EB and AF = FC
To Prove:
(i) EF || BC
(ii) EF = \(\frac{1}{2}\) BC
Construction: Draw a line through C parallel to AB and extend EF which intersect at D.
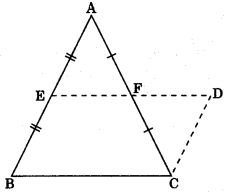
Proof: (i) In AAEF and ACDF,
AF = CF (F is the mid-point of AC)
∠AFE = ∠CFD (Vertically opposite angles)
∠EAF = ∠DCF (Alternate interior angles)
∴ ΔAEF = ΔCDF (by ASA congruency)
∴ AE = CD (by CPCT)
and BE = CD (AE = BE)
EF = FD (by CPCT);
Hence, BCDE is a parallelogram.
ED || BC )
∴ EF || BC
(ii) BCDE is a parallelogram.
DE = BC
EF + FD = BC
2EF = BC
EF=\(\frac{1}{2}\)BC
Converse of Mid-Point Theorem
Theorem 8.10: The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side. ‘
Given: ΔABC in which E is the mid point of AB.
EF || BC
To Prove: AF = FC
Construction: Draw CD || AB and extend EF which intersect at D.
Proof: EF || BC
∴ ED || BC
AB || CD
⇒ BE || CD
∴ BCDE is a parallelogram.
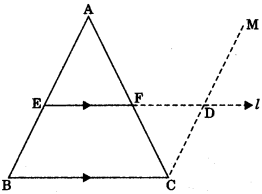
Now in ΔAEF and ΔCDF, ∠AFE = ∠CFD (Vertically opposite angles)
∠EAF = ∠DCF (Alternate interior angles)
AE = CD (BE = AE opposite side of a parallelogram and BE = CD
∴ AAEF ≅ ACDF (by AAS congruency)
Hence AF = FC (by CPCT)